
【题目】如图,在△ABC中,∠BAC=90°,AD是中线,E是AD的中点,过点A作AF∥BC交BE的延长线于F,连接CF.试判断四边形ADCF的形状,并证明你的结论.

【答案】四边形ADCF是菱形,证明见解析
【解析】试题分析:根据AAS证△AFE≌△DBE,利用全等三角形的对应边相等得到AF=BD.结合已知条件,利用“有一组对边平行且相等的四边形是平行四边形”得到ADCF是菱形,由“直角三角形斜边的中线等于斜边的一半”得到AD=DC,从而得出结论.
试题解析:解:四边形ADCF是菱形.理由如下:
∵AF∥BC,∴∠AFE=∠DBE.∵E是AD的中点,AD是BC边上的中线,∴AE=DE,BD=CD.在△AFE和△DBE中,∵∠AFE=∠DBE,∠FEA=∠BED,AE=DE,∴△AFE≌△DBE(AAS),∴AF=DB.∵DB=DC,∴AF=CD.∵AF∥BC,∴四边形ADCF是平行四边形.∵∠BAC=90°,D是BC的中点,∴AD=DC=![]() BC,∴四边形ADCF是菱形.
BC,∴四边形ADCF是菱形.


科目:初中数学 来源: 题型:
【题目】某文艺团体为“希望工程”募捐组织了一场义演,共售出1000张票,筹出票款6920元,且每张成人票8元,学生票5元.
(1)问成人票与学生票各售出多少张?
(2)若票价不变,仍售出1000张票,所得的票款可能是7290元吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的角平分线于点E,交∠BCA的外角平分线于点F.
(1)求证:EO=FO;
(2)当点O运动到何处时,四边形AECF是矩形?并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为倡导低碳生活,绿色出行,某自行车俱乐部利用周末组织“远游骑行”活动.自行车队从甲地出发,途径乙地短暂休息完成补给后,继续骑行至目的地丙地,自行车队出发1小时后,恰有一辆邮政车从甲地出发,沿自行车队行进路线前往丙地,在丙地完成2小时装卸工作后按原路返回甲地,自行车队与邮政车行驶速度均保持不变,并且邮政车行驶速度是自行车队行驶速度的2.5倍,如图表示自行车队、邮政车离甲地的路程y(km)与自行车队离开甲地时间x(h)的函数关系图象,请根据图象提供的信息解答下列各题: 
(1)自行车队行驶的速度是km/h;
(2)邮政车出发多少小时与自行车队首次相遇?
(3)邮政车在返程途中与自行车队再次相遇时的地点距离甲地多远?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,直线PQ垂直平分AC,与边AB交于E,连接CE,过点C作CF平行于BA交PQ于点F,连接AF.
(1)求证:△AED≌△CFD;
(2)求证:四边形AECF是菱形.
(3)若AD=3,AE=5,则菱形AECF的面积是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC的三个顶点的坐标分别为A(﹣5,0)、B(﹣2,3)、C(﹣1,0)
(1)画出△ABC关于坐标原点O成中心对称的△A1B1C1;
(2)将△ABC绕坐标原点O顺时针旋转90°,画出对应的△A′B′C′,
(3)若以A′、B′、C′、D′为顶点的四边形为平行四边形,请直接写出在第四象限中的D′坐标 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一不透明的布袋里,装有红、黄、蓝三种颜色的小球(除颜色外其余都相同),其中有红球2个,蓝球1个,黄球若干个,现从中任意摸出一个球是红球的概率为 ![]() .
.
(1)求口袋中黄球的个数;
(2)甲同学先随机摸出一个小球(不放回),再随机摸出一个小球,请用“树状图法”或“列表法”,求两次摸出都是红球的概率;
(3)现规定:摸到红球得5分,摸到黄球得3分,摸到蓝球得2分(每次摸后放回),乙同学在一次摸球游戏中,第一次随机摸到一个红球第二次又随机摸到一个蓝球,若随机再摸一次,求乙同学三次摸球所得分数之和不低于10分的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=3cm.动点M,N从点C同时出发,均以每秒1cm的速度分别沿CA、CB向终点A,B移动,同时动点P从点B出发,以每秒2cm的速度沿BA向终点A移动,连接PM,PN,设移动时间为t(单位:秒,0<t<2.5).
(1)当t为何值时,以A,P,M为顶点的三角形与△ABC相似?
(2)是否存在某一时刻t,使四边形APNC的面积S有最小值?若存在,求S的最小值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为4,点P为BC边上的任意一点(不与点B、C重合),且∠DPE=90°,PE交AB于点E,设BP=x,BE=y,则y关于x的函数图象大致是( )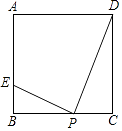
A.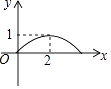
B.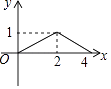
C.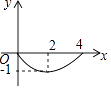
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com