
【题目】如图,直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,且点
,且点![]() 的纵坐标为
的纵坐标为![]() ,直线
,直线![]() 交
交![]() 轴于点
轴于点![]() 将直线
将直线![]() 向上平移
向上平移![]() 个单位得直线
个单位得直线![]() ,交
,交![]() 轴于点
轴于点![]() ,交直线
,交直线![]() 于点
于点![]() 且点
且点![]() 的横坐标为
的横坐标为![]()

(1)求直线![]() 的解析式;
的解析式;
(2)连接![]() 求
求![]() 的面积.
的面积.
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:初中数学 来源: 题型:
【题目】计算:
(1)4992
(2)82018×(﹣0.125)2019
(3)3a2b(﹣![]() a4b2)+(a2b)3
a4b2)+(a2b)3
(4)(a+1)2﹣a(a﹣1)
(5)解二元一次方程组![]()
(6)先化简,再求值:(x+1)2﹣(x﹣1)(x+4),其中x=﹣2.
查看答案和解析>>
科目:初中数学 来源: 题型:
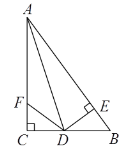
【题目】如图,在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,F在AC上,且BD=DF.
(1)求证:CF=EB;
(2)试判断AB与AF,EB之间存在的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场购进一批日用品,若按每件5元的价格销售,每月能卖出3万件;若按每件6元的价格销售,每月能卖出2万件,假定每月销售件数 ![]() (件)与价格
(件)与价格 ![]() (元/件)之间满足一次函数关系.
(元/件)之间满足一次函数关系.
(1)试求:y与x之间的函数关系式;
(2)这批日用品购进时进价为4元,则当销售价格定为多少时,才能使每月的润最大?每月的最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC= ![]() ,BC=1,D在AC上,将△ADB沿直线BD翻折后,点A落在点E处,如果AD⊥ED,那么△ABE的面积是( )
,BC=1,D在AC上,将△ADB沿直线BD翻折后,点A落在点E处,如果AD⊥ED,那么△ABE的面积是( )
A.1
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一块矩形ABCD的空地上划一块四边形MNPQ进行绿化.如图,四边形的顶点在矩形的边上,且AN=AM=CP=CQ=xcm,已知矩形的边BC=200m,边AB=am,a为大于200的常数,设四边形MNPQ的面积为sm2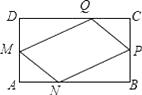
(1)求S关于x的函数关系式,并直接写出自变量x的取值范围.
(2)若a=400,求S的最大值,并求出此时x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB=BC=1,CD=![]() ,DA=1,且∠B=90°.求:
,DA=1,且∠B=90°.求:
(1)∠DAC的度数;
(2)四边形ABCD的面积(结果保留根号);
(3)将△ABC沿AC翻折至△AB′C,如图所示,连接B′D,求△AB′D的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在正方形网格中有一个△ABC,按要求进行下列作图(只能借助于网格).
(1)画出△ABC中BC边上的高AH和BC边上的中线AD.
(2)画出将△ABC向右平移5格又向上平移3格后的△A′B′C′.
(3)△ABC的面积为 .
(4)若连接AA′,CC′,则这两条线段之间的关系是 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com