
【题目】已知四边形ABCD是菱形,AB=4,∠ABC=60°,∠EAF的两边分别与射线CB,DC相交于点E,F,且∠EAF=60°.

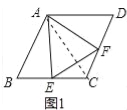
(1)如图1,当点E是线段CB的中点时,直接写出线段AE,EF,AF之间的数量关系;
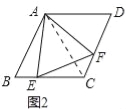
(2)如图2,当点E是线段CB上任意一点时(点E不与B、C重合),求证:BE=CF;
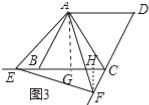
(3)如图3,当点E在线段CB的延长线上,且∠EAB=15°时,求点F到BC的距离.
【答案】(1)AE=EF=AF;(2)证明过程见解析;(3)3-![]()
【解析】
试题分析:(1)结论AE=EF=AF.只要证明AE=AF即可证明△AEF是等边三角形;(2)欲证明BE=CF,只要证明△BAE≌△CAF即可;(3)过点A作AG⊥BC于点G,过点F作FH⊥EC于点H,根据FH=CFcos30°,因为CF=BE,只要求出BE即可解决问题.
试题解析:(1)结论AE=EF=AF.
理由:如图1中,连接AC, ∵四边形ABCD是菱形,∠B=60°, ∴AB=BC=CD=AD,∠B=∠D=60°,
∴△ABC,△ADC是等边三角形, ∴∠BAC=∠DAC=60° ∵BE=EC, ∴∠BAE=∠CAE=30°,AE⊥BC,
∵∠EAF=60°, ∴∠CAF=∠DAF=30°, ∴AF⊥CD, ∴AE=AF(菱形的高相等),
∴△AEF是等边三角形, ∴AE=EF=AF.
(2)如图2中,∵∠BAC=∠EAF=60°, ∴∠BAE=∠CAE,
在△BAE和△CAF中,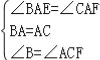 , ∴△BAE≌△CAF, ∴BE=CF.
, ∴△BAE≌△CAF, ∴BE=CF.
(3)过点A作AG⊥BC于点G,过点F作FH⊥EC于点H, ∵∠EAB=15°,∠ABC=60°, ∴∠AEB=45°,
在RT△AGB中,∵∠ABC=60°AB=4, ∴BG=2,AG=2![]() ,在RT△AEG中,∵∠AEG=∠EAG=45°,
,在RT△AEG中,∵∠AEG=∠EAG=45°,
∴AG=GE=2![]() , ∴EB=EG﹣BG=2
, ∴EB=EG﹣BG=2![]() ﹣2, ∵△AEB≌△AFC,
﹣2, ∵△AEB≌△AFC,
∴AE=AF,EB=CF=2![]() ﹣2,∠AEB=∠AFC=45°, ∵∠EAF=60°,AE=AF, ∴△AEF是等边三角形,
﹣2,∠AEB=∠AFC=45°, ∵∠EAF=60°,AE=AF, ∴△AEF是等边三角形,
∴∠AEF=∠AFE=60° ∵∠AEB=45°,∠AEF=60°, ∴∠CEF=∠AEF﹣∠AEB=15°,
在RT△EFH中,∠CEF=15°, ∴∠EFH=75°, ∵∠AFE=60°, ∴∠AFH=∠EFH﹣∠AFE=15°,
∵∠AFC=45°,∠CFH=∠AFC﹣∠AFH=30°, 在RT△CHF中,∵∠CFH=30°,CF=2![]() ﹣2,
﹣2,
∴FH=CFcos30°=(2![]() ﹣2)
﹣2)![]() =3﹣
=3﹣![]() . ∴点F到BC的距离为3﹣
. ∴点F到BC的距离为3﹣![]() .
.


科目:初中数学 来源: 题型:
【题目】在2016年泉州市初中体育中考中,随意抽取某校5位同学一分钟跳绳的次数分别为:158,160,154,158,170,则由这组数据得到的结论错误的是( )
A. 平均数为160 B. 中位数为158 C. 众数为158 D. 方差为20.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在数轴上 A 点表示数 a,B 点示数 b,C 点表示数 c,b 是最大的负整数,且 a、b 满足|a+ 3|+(c﹣6)2=0.
(1)a= ,b= ,c= ;
(2)若将数轴折叠,使得 A点与B 点重合,则点 C与数 表示的点重合;
(3)点 A、B、C开始在数轴上运动,若点 A以每秒 2个单位长度的速度向左运动,同时,点 B和 点 C分别以每秒1个单位长度和 4个单位长度的速度向右运动,假设 t 秒钟过后,若点 A与点 B之间的距离表示为 AB,点 A与点 C之间的距离表示为 AC,点 B与点 C之间的距离表示为 BC.则 AB= ,AC= ,BC= .(用 含 t的代数式表示)
(4)请问:2BC+AB - ![]() AC的值是否随着时间 t 的变化而改变?若变化,请说明理由;若不变,请求其值.
AC的值是否随着时间 t 的变化而改变?若变化,请说明理由;若不变,请求其值.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图一,抛物线y=ax2+bx+c与x轴正半轴交于A、B两点,与y轴交于点C,直线y=x-2经过A、C两点,且AB=2.
(1)求抛物线的解析式;
(2)若直线DE平行于x轴并从C点开始以每秒1个单位的速度沿y轴正方向平移,且分别交y轴、线段BC于点E,D,同时动点P从点B出发,沿BO方向以每秒2个单位速度运动,(如图2);当点P运动到原点O时,直线DE与点P都停止运动,连DP,若点P运动时间为t秒;设s=![]() ,当t为何值时,s有最小值,并求出最小值.
,当t为何值时,s有最小值,并求出最小值.
(3)在(2)的条件下,是否存在t的值,使以P、B、D为顶点的三角形与△ABC相似;若存在,求t的值;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
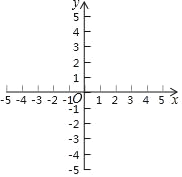
【题目】已知函数y=﹣x+4,回答下列问题:
(1)请在右图的直角坐标系中画出函数y=﹣x+4图象;
(2)y的值随x值的增大而________;
(3)当y=2时,x的值为_________;
(4)当y<0时,x的取值范围是_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在数轴上A点表示数a,B点示数b,C点表示数c,b是最小的正整数,且a,b满足![]() +(c-7)2=0.
+(c-7)2=0.
(1) a= ,b= ,c= .
(2) 若将数轴折叠,使得A点与C点重合,则点B与数 表示的点重合.
(3) 点A,B,C开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒2个单位长度和4个单位长度的速度向右运动,假设t秒钟过后,若点A与点B之间的距离表示为AB,点A与点C之间的距离表示为AC,点B与点C之间的距离表示为BC.则AB= ,AC= ,BC= .(用含t的代数式表示)
(4) 请问:3BC-2AB的值是否随着时间t的变化而改变? 若变化,请说明理由;若不变,请求其值.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】检修小组从A地出发,在东西路上检修线路,若规定向东行驶的路程为正数,向西行驶的路程为负数,一天中行驶记录(单位;千米)如下: ![]()
(1)收工时检修小组在A地的哪侧,距A地多远?
(2)若每千米耗油0.3升,从出发到收工共耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司准备投资开发A、B两种新产品,通过市场调研发现:如果单独投资A种产品,则所获利润yA(万元)与投资金额x(万元)之间满足正比例函数关系:yA=kx;如果单独投资B种产品,则所获利润yB(万元)与投资金额x(万元)之间满足二次函数关系:yB=ax2+bx.根据公司信息部的报告,yA、yB(万元)与投资金额x(万元)的部分对应值(如下表)

(1)求正比例函数和二次函数的解析式;
(2)如果公司准备投资20万元同时开发A、B两种新产品,请你设计一个能获得最大利润的投资方案,并求出按此方案能获得的最大利润是多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
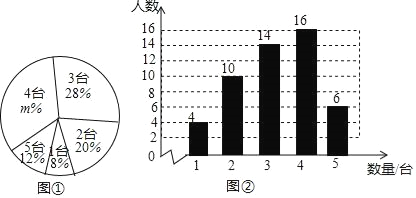
【题目】随着移动计算技术和无线网络的快速发展,移动学习方式越来越引起人们的关注,某校计划将这种学习方式应用到教育学中,从全校1500名学生中随机抽取了部分学生,对其家庭中拥有的移动设备的情况进行调查,并绘制出如下的统计图①和图②,根据相关信息,解答下列问题:
(1)本次接受随机抽样调查的学生人数为 ,图①中m的值为 ;
(2)求本次调查获取的样本数据的众数、中位数和平均数;
(3)根据样本数据,估计该校1500名学生家庭中拥有3台移动设备的学生人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com