
 如图,直线AB、CD相交于点O,OE平分∠BOD,OF平分∠COE,∠AOD:∠BOE=4:1,则∠AOF的度数为( )
如图,直线AB、CD相交于点O,OE平分∠BOD,OF平分∠COE,∠AOD:∠BOE=4:1,则∠AOF的度数为( )| A. | 120° | B. | 125° | C. | 130° | D. | 135° |
分析 设∠BOE=x°,则∠AOD=4x°,由OE平分∠BOD得∠BOE=∠DOE=x°,根据∠AOD+∠BOD=180°列方程求得x,继而可得∠AOC、∠COE度数,根据OF平分∠COE得∠COF,由∠AOF=∠AOC+∠COF可得答案.
解答 解:设∠BOE=x°,则∠AOD=4x°,
∵OE平分∠BOD,
∴∠BOE=∠DOE=x°,
∴∠AOC=∠BOD=2x°,
∵∠AOD+∠BOD=180°,
∴4x+2x=180,解得:x=30,
∴∠COE=∠COD-∠DOE=180°-30°=150°,
∵OF平分∠COE,
∴∠COF=$\frac{1}{2}$∠COE=75°,
∴∠AOF=∠AOC+∠COF=60°+75°=135°,
故选:D.
点评 本题主要考查角平分线定义、邻补角及对顶角性质,设出最小角根据邻补角定义求得最小角度数是解题的关键.


 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,一艘轮船在A处测得北偏东45°方向有一灯塔B,船向正东方向航行到达C处时,又观测到灯塔B在北偏东30°方向上,此时轮船与灯塔相距60海里,求轮船从A处到C处航行了多少海里(结果保留根号).
如图,一艘轮船在A处测得北偏东45°方向有一灯塔B,船向正东方向航行到达C处时,又观测到灯塔B在北偏东30°方向上,此时轮船与灯塔相距60海里,求轮船从A处到C处航行了多少海里(结果保留根号).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 2002 年国际数学家大会在中国北京举行,这是21 世纪全世界数学家的第一次大聚会.这次大会的会徽就是如图,选定的是我国古代数学家赵爽用来证明勾股定理的弦图,可以说是充分肯定了我国数学的成就,也弘扬了我国古代的数学文化.弦图是由四个全等的直角三角形和中间的 小正方形拼成的一个大正方形.如果大正方形的面积是13,小正方形的面积是1,直角三角形的较短直角边长为a,较长直角边长为b,那么你能求出(a+b)2 的值吗?
2002 年国际数学家大会在中国北京举行,这是21 世纪全世界数学家的第一次大聚会.这次大会的会徽就是如图,选定的是我国古代数学家赵爽用来证明勾股定理的弦图,可以说是充分肯定了我国数学的成就,也弘扬了我国古代的数学文化.弦图是由四个全等的直角三角形和中间的 小正方形拼成的一个大正方形.如果大正方形的面积是13,小正方形的面积是1,直角三角形的较短直角边长为a,较长直角边长为b,那么你能求出(a+b)2 的值吗?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①②③ | B. | ①③ | C. | ①② | D. | ②③ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | AB=DE,∠C=∠F,∠B=∠E | B. | BC=DE,AC=DF,∠C=∠D | ||
| C. | AB=DE,∠B=∠E,AC=DF | D. | AB=EF,∠B=∠F,∠A=∠E |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
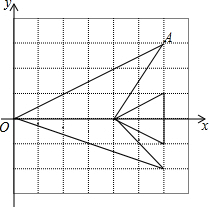 如图,将平面直角坐标系中“鱼”的每个“顶点”的纵坐标保持不变,横坐标变为原来的$\frac{1}{2}$,那么点A对应的点A′的坐标是(3,3).
如图,将平面直角坐标系中“鱼”的每个“顶点”的纵坐标保持不变,横坐标变为原来的$\frac{1}{2}$,那么点A对应的点A′的坐标是(3,3).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com