
【题目】如图,已知点B、C、D在同一条直线上,△ABC和△CDE都是等边三角形.BE交AC于F,AD交CE于H,求证:
(1)△BCE≌△ACD;
(2)CF=CH;
(3)△FCH是等边三角形;
(4)FH∥BD.
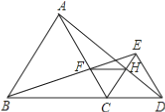
【答案】见解析
【解析】试题分析:(1)由等边三角形的三边相等,三角都是60°,再根据平角的关系,就能证明△BCE≌△ACD;(2)由△BCE≌△ACD得出对应角相等,结合等边三角形的边角特点证明△BCF≌△ACH,能得出CF=CH;(3)两边等,加上一个角60°推出△CFH是等边三角形;(4)根据内错角相等,两直线平行推出FH∥BD.
试题解析:
证明:∵△ABC和△CDE都是等边三角形,
∴∠BCA=∠DCE=60°,BC=AC=AB,EC=CD=ED,
∴∠BCE=∠ACD.
在△BCE和△ACD中,

∴△BCE≌△ACD(SAS);
(2)∵△BCE≌△ACD,
∴∠CBF=∠CAH.
∵∠ACB=∠DCE=60°,
在△BCF和△ACH中,
∴∠ACH=60°,
∴∠BCF=∠ACH,

∴△BCF≌△ACH(ASA),
∴CF=CH;
(3)∵CF=CH,∠ACH=60°,
∴△CFH是等边三角形.
(4)∵△CHF为等边三角形
∴∠FHC=60°,
∵∠HCD=60°,
∴FH∥BD


科目:初中数学 来源: 题型:
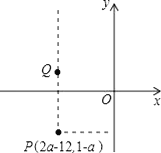
【题目】已知点P(2a﹣12,1﹣a)位于第三象限,点Q(x,y)位于第二象限且是由点P向上平移一定单位长度得到的.
(1)若点P的纵坐标为﹣3,试求出a的值;
(2)在(1)题的条件下,试求出符合条件的一个点Q的坐标;
(3)若点P的横、纵坐标都是整数,试求出a的值以及线段PQ长度的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣x+3与x轴交于点C,与y轴交于点B,抛物线y=ax2+ ![]() x+c经过B、C两点,点E是直线BC上方抛物线上的一动点.
x+c经过B、C两点,点E是直线BC上方抛物线上的一动点.
(1)求抛物线的解析式;
(2)过点E作y轴的平行线交直线BC于点M、交x轴于点F,当S△BEC= ![]() 时,请求出点E和点M的坐标;
时,请求出点E和点M的坐标;
(3)在(2)的条件下,当E点的横坐标为1时,在EM上是否存在点N,使得△CMN和△CBE相似?如果存在,请直接写出点N的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的面积为2 ![]() cm2 , 对角线交于点O1 , 以AB、AO1为邻边做平行四边形AO1C1B,对角线交于点O2 , 以AB、AO2为邻边做平行四边形AO2C2B,…,以此类推,则平行四边形AO6C6B的面积为cm2 .
cm2 , 对角线交于点O1 , 以AB、AO1为邻边做平行四边形AO1C1B,对角线交于点O2 , 以AB、AO2为邻边做平行四边形AO2C2B,…,以此类推,则平行四边形AO6C6B的面积为cm2 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用10个球设计一个摸球游戏,使得:
(1)摸到红球的机会是![]() .
.
(2)摸到红球的机会是![]() ,摸到黄球的机会是
,摸到黄球的机会是![]() .
.
(3)你还能设计一个符合下列条件的游戏吗?为什么?
摸到红球的机会是![]() ,摸到黄球的机会是
,摸到黄球的机会是![]() ,摸到绿球的机会是
,摸到绿球的机会是![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】冠状病毒有多种类型,新型冠状病毒也是其中的一种.冠状病毒的直径在60﹣220纳米之间,平均直径为100纳米左右(1纳米=10﹣9米).那么100纳米可用科学记数法表示为( )
A.100×10﹣9米B.100×109米C.1×10﹣7米D.1×107米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,给出下列三个论断:①∠B+∠D=180°;②AB∥CD;③BC∥DE.(1)在上述三个论断中,以其中两个论断作为条件,另外一个论断作结论,写出一个正确的命题,并加以证明。
命题:如果____________________那么____________________
证明:

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,以△ABC的边AB为直径作⊙O,点C在⊙O上,BD是⊙O的弦,∠A=∠CBD,过点C作CF⊥AB于点F,交BD于点G,过C作CE∥BD交AB的延长线于点E.
(1)求证:CE是⊙O的切线;
(2)求证:CG=BG;
(3)若∠DBA=30°,CG=4,求BE的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com