
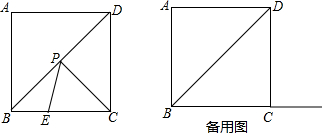
分析 (1)根据正方形的对角线平分一组对角,且四个角为直角,确定出所求角度数即可;
(2)连接AP,当AP与PE在一条线上时,PE+PC最小,利用勾股定理求出最小值;当P与B重合时,|PE-PC|最大,表示出最大值即可;
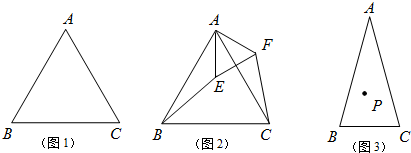
(3)分两种情况考虑:①当E在BC延长线上时,如图2所示,△PCE为等腰三角形,则CP=CE;②当E在BC上,如图3所示,△PCE是等腰三角形,则PE=CE,分别求出∠PEC的度数即可.
解答 解:(1)∠PBC=45度;
故答案为:45;
(2)如图1所示:当AP与PE在一条线上时,PE+PC最小,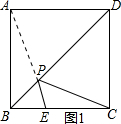
∵AB=4,BE=t,
∴PE+PC的最小值为$\sqrt{16+{t^2}}$;
当P与B重合时,|PE-PC|的最大值,最大值是|4-t|;
故答案为:$\sqrt{16+{t}^{2}}$;|4-t|;
(3)分两种情况考虑:
①当点E在BC的延长线上时,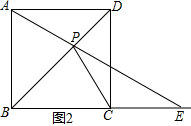
如图2所示,△PCE是等腰三角形,则CP=CE,
∴∠CPE=∠CEP,
∴∠BCP=∠CPE+∠CEP=2∠CEP,
∵在正方形ABCD中,∠ABC=90°,
∴∠PBA=∠PBC=45°,
在△ABP和△CBP中,
$\left\{\begin{array}{l}{AB=BC}\\{∠ABP=∠CBP}\\{BP=BP}\end{array}\right.$,
∴△ABP≌△CBP(SAS),
∴∠BAP=∠BCP=2∠CEP,
∵∠BAP+∠PEC=90°,
∴2∠PEC+∠PEC=90°,
∴∠PEC=30°;
②当点E在BC上时,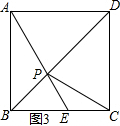
如图3所示,△PCE是等腰三角形,则PE=CE,
∴∠CPE=∠PCE,
∴∠BEP=∠CPE+∠PCE=2∠ECP,
∵四边形ABCD是正方形,
∴∠PBA=∠PBC=45°,
又AB=BC,BP=BP,
∴△ABP≌△CBP,
∴∠BAP=∠BCP,
∵∠BAP+∠AEB=90°,
∴2∠BCP+∠BCP=90°,
∴∠BCP=30°,
∴∠AEB=60°,
∴∠PEC=180°-∠AEB=120°,
综上所述:当△PCE为等腰三角形时,∠PEC的度数为30°或120°.
点评 此题属于四边形综合题,涉及的知识有:正方形的性质,等腰三角形的性质,全等三角形的判定与性质,以及三角形内角和定理,熟练掌握性质及定理是解本题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | 一批炮弹的杀伤力的情况 | B. | 了解一批灯泡的使用寿命 | ||
| C. | 全面人口普查 | D. | 全市学生每天参加体育锻炼的时间 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
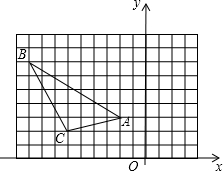 如图,在直角坐标系中,△ABC的顶点都在网格点上(方格纸中每个小正方形边长为1),将△ABC向右平移4格,再向下平移2格.
如图,在直角坐标系中,△ABC的顶点都在网格点上(方格纸中每个小正方形边长为1),将△ABC向右平移4格,再向下平移2格.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com