
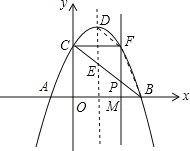
【题目】如图,抛物线![]() 与
与![]() 轴相交于A、B两点(点A在点B的左侧),与y轴相交于点C,顶点为D.
轴相交于A、B两点(点A在点B的左侧),与y轴相交于点C,顶点为D.
(1)直接写出A、B、C三点的坐标和抛物线的对称轴;
(2)连接![]() ,与抛物线的对称轴交于点
,与抛物线的对称轴交于点![]() ,点
,点![]() 为线段
为线段![]() 上的一个动点,过点
上的一个动点,过点![]() 作PF∥DE交抛物线于点F,设点P的横坐标为m;
作PF∥DE交抛物线于点F,设点P的横坐标为m;
①用含m的代数式表示线段PF的长,并求出当m为何值时,四边形PEDF为平行四边形?
②设△BCF的面积为S,求S与m的函数关系式,S是否有最大值?如有,请求出最大值,没有请说明理由.


【答案】(1) A(1,0),B(3,0),C(0,3),抛物线对称轴为直线x=1 ;(2)①PF=m2+3m,m=2;②S=![]() ;当m=
;当m=![]() 时,S取得最大值为
时,S取得最大值为![]() .
.
【解析】试题分析:(1)已知了抛物线的解析式,当y=0时可求出A,B两点的坐标,当x=0时,可求出C点的坐标.根据对称轴x=![]() 可得出对称轴的解析式;(2)①根据B,C的坐标求出BC所在直线的解析式,然后将m分别代入直线BC和抛物线的解析式中,求得出两函数的值的差就是PF的长.根据直线BC的解析式,可得出E点的坐标,根据抛物线的解析式可求出D点的坐标,求出DE的长,然后让PF=DE,即可求出此时m的值.②根据△BCF的面积=△PFC的面积+△PFB的面积,即可求出关于S、m的函数关系式,利用二次函数的性质求得最大值即可.
可得出对称轴的解析式;(2)①根据B,C的坐标求出BC所在直线的解析式,然后将m分别代入直线BC和抛物线的解析式中,求得出两函数的值的差就是PF的长.根据直线BC的解析式,可得出E点的坐标,根据抛物线的解析式可求出D点的坐标,求出DE的长,然后让PF=DE,即可求出此时m的值.②根据△BCF的面积=△PFC的面积+△PFB的面积,即可求出关于S、m的函数关系式,利用二次函数的性质求得最大值即可.
试题解析:
(1)A(1,0),B(3,0),C(0,3),抛物线对称轴为直线x=1;
(2)①设直线BC的函数解析式为y=kx+b,
把B(3,0),C(0,3)分别代入得:
![]() ,
,
解得:k=1,b=3,
∴直线BC的解析式为y=x+3,
当x=1时,y=1+3=2,
∴E(1,2),
当x=m时,y=m+3,
∴P(m,m+3),
令y=x2+2x+3中x=1,得到y=4,∴D(1,4),
当x=m时,y=m2+2m+3,∴F(m,m2+2m+3),
∴线段DE=42=2,
∵0<m<3,∴线段PF=m2+2m+3(m+3)=m2+3m,
连接DF,由PF∥DE,得到当PF=DE时,四边形PEDF为平行四边形,
由m2+3m=2,得到m=2或m=1(不合题意,舍去),
则当m=2时,四边形PEDF为平行四边形;
②连接BF、CF,设直线PF与x轴交于点M,由B(3,0) ,O(0,0),
可得OB=OM+MB=3,
∵S=S△BPF+S△CPF=![]() PFBM+
PFBM+![]() PFOM=
PFOM=![]() PF(BM+OM)=
PF(BM+OM)= ![]() PFOB,
PFOB,
∴S=![]() ×3(m2+3m)=
×3(m2+3m)= ![]() m2+
m2+![]() m=
m=![]() (0<m<3),
(0<m<3),
则当m=![]() 时,S取得最大值为
时,S取得最大值为![]() .
.


 寒假学与练系列答案
寒假学与练系列答案科目:初中数学 来源: 题型:
【题目】某校为加强学生安全意识,组织全校学生参加安全知识竞赛。从中抽取部分学生成绩(得分取正整数值,满分为100分)进行统计,绘制以下两幅不完整的统计图.

请根据图中的信息,解决下列问题:
(1)填空:a=_____,n=_____;
(2)补全频数直方图;
(3)该校共有2000名学生.若成绩在70分以下(含70分)的学生安全意识不强,则该校安全意识不强的学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A、B以及直线l,AE⊥l,垂足为点E.
(1)尺规作图:①过点B作BF⊥l,垂足为点F
②在直线l上求作一点C,使CA=CB;(要求:在图中标明相应字母,保留作图痕迹,不写作法)
(2)在所作的图中,连接CA、CB,若∠ACB=90°,∠CAE=![]() ,则∠CBF= (用含
,则∠CBF= (用含![]() 的代数式表示)
的代数式表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“构造图形解题”,它的应用十分广泛,特别是有些技巧性很强的题目,如果不能发现题目中所隐含的几何意义,而用通常的代数方法去思考,经常让我们手足无措,难以下手,这时,如果能转换思维,发现题目中隐含的几何条件,通过构造适合的几何图形,将会得到事半功倍的效果,下面介绍两则实例:
实例一:1876年,美国总统伽非尔德利用实例一图证明了勾股定理:由
S四边形ABCD=S△ABC+S△ADE+S△ABE得![]() ,化简得:
,化简得:![]()
实例二:欧几里得的《几何原本》记载,关于x的方程![]() 的图解法是:
的图解法是:
画Rt△ABC,使∠ABC=90°,BC=![]() ,AC=
,AC=![]() ,再在斜边AB上截取BD=
,再在斜边AB上截取BD=![]() ,则AD的长就是该方程的一个正根(如实例二图)
,则AD的长就是该方程的一个正根(如实例二图)
请根据以上阅读材料回答下面的问题:
(1)如图1,请利用图形中面积的等量关系,写出甲图要证明的数学公式是 ,乙图要证明的数学公式是
(2)如图2,若2和-8是关于x的方程x2+6x=16的两个根,按照实例二的方式构造Rt△ABC,连接CD,求CD的长;
(3)若x,y,z都为正数,且x2+y2=z2,请用构造图形的方法求![]() 的最大值.
的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
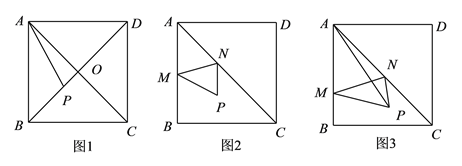
【题目】问题探究:在边长为![]() 的正方形
的正方形![]() 中,对角线
中,对角线![]() 、
、![]() 交于点
交于点![]() .
.
探究![]() :如图
:如图![]() ,若点
,若点![]() 是对角线
是对角线![]() 上任意一点,则线段
上任意一点,则线段![]() 的长的取值范围是__________;
的长的取值范围是__________;
探究![]() :如图
:如图![]() ,若点
,若点![]() 是
是![]() 内任意一点,点
内任意一点,点![]() 、
、![]() 分别是
分别是![]() 边和对角线
边和对角线![]() 上的两个动点,则当
上的两个动点,则当![]() 的值在探究
的值在探究![]() 中的取值范围内变化时,
中的取值范围内变化时, ![]() 的周长是否存在最小值?如果存在,请求出
的周长是否存在最小值?如果存在,请求出![]() 周长的最小值,若不存在,请说明理由;
周长的最小值,若不存在,请说明理由;
问题解决:如图![]() ,在边长为
,在边长为![]() 的正方形
的正方形![]() 中,点
中,点![]() 是
是![]() 内任意一点,且
内任意一点,且![]() ,点
,点![]() 、
、![]() 分别是
分别是![]() 边和对角线
边和对角线![]() 上的两个动点,则当
上的两个动点,则当![]() 的周长取到最小值时,求四边形
的周长取到最小值时,求四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AD是△ABC的角平分线,CE是△ABC的高,AD与CE相交于点P,∠BAC=66°,∠BCE=40°,求∠ADC和∠APC的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在面积为3的△ABC中,AB=3,∠BAC=45°,点D是BC边上一点.
(1)若AD是BC边上的中线,求AD的长;
(2)点D关于直线AB和AC的对称点分别为点M、N,求AN的长度的最小值;
(3)若P是△ABC内的一点,求![]() 的最小值.
的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列结论中,错误结论有( );①三角形三条高(或高的延长线)的交点不在三角形的内部,就在三角形的外部;②一个多边形的边数每增加一条,这个多边形的内角和就增加360;③两条平行直线被第三条直线所截,同旁内角的角平分线互相平行;④三角形的一个外角等于任意两个内角的和;⑤在![]() 中,若
中,若![]() ,则
,则![]() 为直角三角形;⑥顺次延长三角形的三边,所得的三角形三个外角中锐角最多有一个
为直角三角形;⑥顺次延长三角形的三边,所得的三角形三个外角中锐角最多有一个
A. 6个B. 5个C. 4个D. 3个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com