
 已知:如图所示,在正方形ABCD中,E为AD的中点,F为DC上的一点,且DF=
已知:如图所示,在正方形ABCD中,E为AD的中点,F为DC上的一点,且DF=| 1 | 4 |
科目:初中数学 来源: 题型:
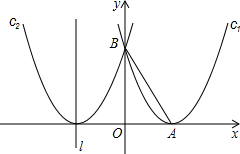 已知,如图所示,抛物线c1:y=ax2+bx+c的顶点A在x轴的正半轴上,并与y轴交于点B,OA=
已知,如图所示,抛物线c1:y=ax2+bx+c的顶点A在x轴的正半轴上,并与y轴交于点B,OA=| 3 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 12、如图所示,在大房间的一面墙壁上,边长为15cm的正六边形A(如图(1))横排20块和以其一部分所形成的梯形B,三角形C,D,E,菱形F等六种瓷砖毫无空隙地排列在一起,已知墙壁高3.3m,请你仔细观察各层瓷砖的排列特点,计算其中菱形F瓷砖需使用
12、如图所示,在大房间的一面墙壁上,边长为15cm的正六边形A(如图(1))横排20块和以其一部分所形成的梯形B,三角形C,D,E,菱形F等六种瓷砖毫无空隙地排列在一起,已知墙壁高3.3m,请你仔细观察各层瓷砖的排列特点,计算其中菱形F瓷砖需使用查看答案和解析>>
科目:初中数学 来源: 题型:
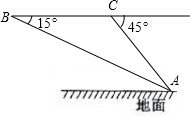 俯角为45°,已知歼10战斗机的飞行速度为600米/秒.求飞机距地面飞行的高度?(结果精确到0.1米)
俯角为45°,已知歼10战斗机的飞行速度为600米/秒.求飞机距地面飞行的高度?(结果精确到0.1米)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
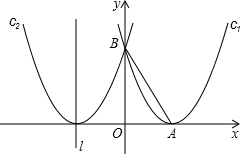 已知,如图所示,抛物线c1:y=ax2+bx+c的顶点A在x轴的正半轴上,并与y轴交于点B,OA=
已知,如图所示,抛物线c1:y=ax2+bx+c的顶点A在x轴的正半轴上,并与y轴交于点B,OA= ,AB=
,AB= ,抛物线c2与抛物线c1关于y轴对称.
,抛物线c2与抛物线c1关于y轴对称.查看答案和解析>>
科目:初中数学 来源:2010年广东省深圳市宝安区中考数学三模试卷(解析版) 题型:解答题
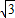 ,AB=
,AB=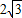 ,抛物线c2与抛物线c1关于y轴对称.
,抛物线c2与抛物线c1关于y轴对称.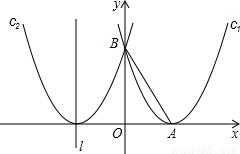
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com