
【题目】某校240名学生参加植树活动,要求每人植树4~7棵,活动结束后抽查了20名学生每人的植树量,并分为四类:A类4棵、B类5棵、C类6棵、D类7棵,将各类的人数绘制成如图所示不完整的条形统计图,回答下列问题:
(1)补全条形图;
(2)写出这20名学生每人植树量的众数和中位数;
(3)估计这240名学生共植树多少棵?
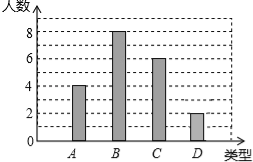
【答案】(1)图形见解析
(2)众数为5,中位数是5;
(3)估计这240名学生共植树1272棵.
【解析】试题分析:(1)先求出D类的人数,然后补全统计图即可;
(2)由众数的定义解答,根据中位数的定义,因为是20个人,因此找出第10人和第11人植树的棵树,求出平均数即为中位数;
(3)求出20人植树的平均棵树,然后乘以总人数240计算即可得解.
试题解析:(1)D类的人数为:20﹣4﹣8﹣6=20﹣18=2人,
补全统计图如图所示;
(2)由图可知,植树5棵的人数最多,是8人,
所以,众数为5,
按照植树的棵树从少到多排列,第10人与第11人都是植5棵数,
所以,中位数是5;
(3)![]() =5.3(棵),
=5.3(棵),
240×5.3=1272(棵).
答:估计这240名学生共植树1272棵.


 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:
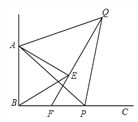
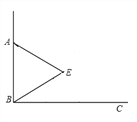
【题目】如图,已知∠ABC=90°,△ABE是等边三角形,点P为射线BC上任意一点(点P与点B不重合),连接AP,将线段AP绕点A逆时针旋转60°得到线段AQ,连接QE并延长交射线BC于点F.
(1)如图,当BP=BA时,∠EBF=______°,猜想∠QFC =______°;
(2)如图,当点P为射线BC上任意一点时,猜想∠QFC的度数,并加以证明.
(3)已知线段AB=![]() ,设BP=x,点Q到射线BC的距离为y,求y关于x的函数关系式.
,设BP=x,点Q到射线BC的距离为y,求y关于x的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各式由左边到右边的变形中,是因式分解的为( )
A. m(x+y)=mx+myB. 8x2﹣4x=4x(2x﹣1)
C. x2﹣6x+5=x(x﹣6)+5D. x2﹣9+2x=(x+3)(x﹣3)+2x
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如图,图象过点(﹣1,0),对称轴为直线x=2,下列结论:
①4a+b=0;②9a+c>3b;③8a+7b+2c>0;④当x>﹣1时,y的值随x值的增大而增大;⑤当函数值y<0时,自变量x的取值范围是x<-1或x>5.
其中正确的结论有( )

A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AE∥BF,AC平分∠BAE,且交BF于点C,BD平分∠ABF,且交AE于点D,AC与BD相交于点O,连接CD
(1)求∠AOD的度数;
(2)求证:四边形ABCD是菱形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,按如下步骤作图:
①分别以A,C为圆心,大于![]() 的长为半径画弧,两弧交于P,Q两点;
的长为半径画弧,两弧交于P,Q两点;
②作直线PQ,分别交AB,AC于点E,D,连接CE;
③过C作CF∥AB交PQ于点F,连接AF.
(1)求证:△AED≌△CFD;
(2)求证:四边形AECF是菱形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】宁波轨道交通4号线已开工建设,计划2020年通车试运营。为了了解镇民对4号线地铁票的定价意向,某镇某校数学兴趣小组开展了“你认为宁波4号地铁起步价定为多少合适”的问卷调查,并将调查结果整理后制成了如下统计图,根据图中所给出的信息解答下列问题:
(1)求本次调查中该兴趣小组随机调查的人数;
(2)请你把条形统计图补充完整;
(3)如果在该镇随机咨询一位居民,那么该居民支持“起步价为2元或3元”的概率是____
(4)假设该镇有3万人,请估计该镇支持“起步价为3元”的居民大约有多少人?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com