
| 种子个数 | 100 | 200 | 300 | 400 | 500 | 600 | 700 | 800 | 900 | 1000 |
| 发芽种子个数 | 94 | 187 | 282 | 338 | 435 | 530 | 624 | 718 | 814 | 901 |
| 发芽种子频率 | 0.940 | 0.935 | 0.940 | 0.845 | 0.870 | 0.883 | 0.891 | 0.898 | 0.904 | 0.901 |
科目:初中数学 来源: 题型:填空题
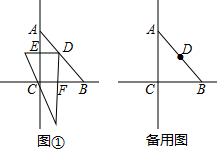
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
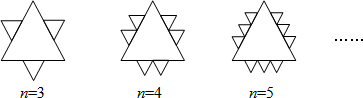
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
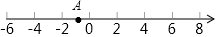 如图,已知点A在数轴上,从点A出发,沿数轴向右移动3个单位长度到达点C,点B所表示的有理数是5的相反数,按要求完成下列各小题.
如图,已知点A在数轴上,从点A出发,沿数轴向右移动3个单位长度到达点C,点B所表示的有理数是5的相反数,按要求完成下列各小题.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
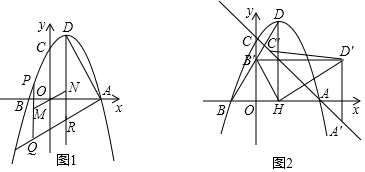
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com