
【题目】某环卫公司承包了市区两个片区道路的清扫任务,需要购买某厂家A,B两种型号的马路清扫车,购买5辆A型马路清扫车和6辆B型马路清扫车共需171万元;购买3辆A型马路清扫车和12辆B型马路清扫车共需237万元.
(1)求这两种马路清扫车的单价;
(2)恰逢该厂举行30周年庆,决定对这两种马路清扫车开展促销活动,具体方案如下:购买A型马路清扫车按原价的八折销售,购买B型马上清扫车不超过10辆时按原价销售,超过10辆的部分按原价的七折销售.设购买x辆A种马路清扫车需要y1元,购买x(x>0)个B型马路清扫车需要y2元,分别求出y1,y2关于x的函数关系式;
(3)若该公司承包的道路清扫面积为118000m2,每辆A型马路清扫车每天清扫5000m2,每辆B型马路清扫车每天清扫6000m2,公司准备购买20辆马路清扫车,且B型马路清扫车的数量大于10.请你帮该公司设计出最省钱的购买方案.请说明理由.
【答案】(1)A型马路清扫车的单价为15万元,B型马路清扫车的单价为16万元;(2)y1=12x,当0<x≤10时,y2=16x;当x>10时,y2=11.2x+48;(3)该公司购买A型马路清扫车2辆,购买B型马路清扫车18辆时最省钱,最低费用为273.6万元.
【解析】
(1)设A型马路清扫车的单价为a万元,B型马路清扫车的单价为b万元,根据“购买5辆A型马路清扫车和6辆B型马路清扫车共需171万元;购买3辆A型马路清扫车和12辆B型马路清扫车共需237万元”即可得出关于a、b的二元一次方程组,解方程组即可得出结论;
(2)根据“A型马路清扫车按原价的八折销售,购买B型马上清扫车不超过10辆时按原价销售,超过10辆的部分按原价的七折销售”,即可得出y1、y2关于x的函数关系式;
(3)设该公司购买B型马路清扫车m辆,则购买A型马路清扫车(20m)辆,根据题意求出m的取值范围,即可解答.
(1)设A型马路清扫车的单价为a万元,B型马路清扫车的单价为b万元,
则由题意可知:![]() ,解得
,解得![]() ,
,
答:A型马路清扫车的单价为15万元,B型马路清扫车的单价为16万元;
(2)由题意可知:y1=0.8×15x,即y1=12x,
当0<x≤10时,y2=16x;
当x>10时,y2=16×10+16(x﹣10)×0.7,即y2=11.2x+48.
∴y2=![]() ;
;
(3)设该公司购买B型马路清扫车m辆,则购买A型马路清扫车(20﹣m)辆,
根据题意得,![]() ,
,
解得m≥18,
∵A型马路清扫车的单价比B型马路清扫车的单价便宜,
∴m=18时,该公司最省钱,此时购买总费用为:15×0.8×(20﹣18)+16×10+16×0.7×(18﹣10)=273.6(万元).
即该公司购买A型马路清扫车2辆,购买B型马路清扫车18辆时最省钱,最低费用为273.6万元.


 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:
【题目】为了解某校学生对《最强大脑》、《朗读者》、《中国诗词大会》、《出彩中国人》四个电视节目的喜爱情况,随杋抽取了![]() 名学生进行调查统计(要求每名学生选出并且只能选出一个自己最喜爱的节目),并将调查结果绘制成如图统计图表:
名学生进行调查统计(要求每名学生选出并且只能选出一个自己最喜爱的节目),并将调查结果绘制成如图统计图表:
学生最喜爱的节目人数统计表
节目 | 人数(名) | 百分比 |
最强大脑 |
|
|
朗读者 |
|
|
中国诗词大会 |
|
|
出彩中国 |
|
|

根据以上提供的信息,解答下列问题:
(1)![]() ______,
______,![]() _____,
_____,![]() ____;
____;
(2)补全上面的条形统计图;
(3)若该校共有学生5000名,根据抽样调查结果,估计该校最喜爱《中国诗词大会》节目的学生有多少名.
查看答案和解析>>
科目:初中数学 来源: 题型:
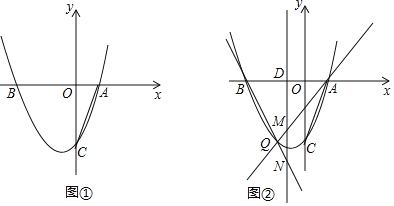
【题目】如图,抛物线y=x2+bx+c交x轴于A、B两点,其中点A坐标为(1,0),与y轴交于点C(0,﹣3).
(1)求抛物线的函数表达式;
(2)如图①,连接AC,点P在抛物线上,且满足∠PAB=2∠ACO.求点P的坐标;
(3)如图②,点Q为x轴下方抛物线上任意一点,点D是抛物线对称轴与x轴的交点,直线AQ、BQ分别交抛物线的对称轴于点M、N.请问DM+DN是否为定值?如果是,请求出这个定值;如果不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
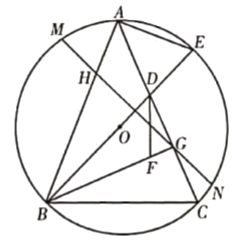
【题目】已知: ![]() 是
是![]() 的两条弦,
的两条弦,![]() 于点
于点![]() ,
,![]() 的平分线交
的平分线交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]()
![]() 如图1,求
如图1,求![]() 的度数;
的度数;

![]() 如图2,
如图2,![]() 为
为![]() 上一点,连接
上一点,连接![]() ,当
,当![]() 时,求证:
时,求证:![]()

![]() 如图3 ,在
如图3 ,在![]() 的条件下,当
的条件下,当![]() 为
为![]() 的直径时,经过点
的直径时,经过点![]() 的弦
的弦![]() 交
交![]() 于点
于点![]() ,若
,若![]() 的面积为
的面积为![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,n),且与x轴的一个交点在点(3,0)和(4,0)之间.则下列结论:①a﹣b+c>0;②3a+b=0;③b2=4a(c﹣n);④一元二次方程ax2+bx+c=n﹣1有两个不相等的实数根.其中正确结论的是______________(只填序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:关于x的方程![]()
(1)求证:m取任何值时,方程总有实根.
(2)若二次函数![]() 的图像关于y轴对称.
的图像关于y轴对称.
a、求二次函数![]() 的解析式
的解析式
b、已知一次函数![]() ,证明:在实数范围内,对于同一x值,这两个函数所对应的函数值
,证明:在实数范围内,对于同一x值,这两个函数所对应的函数值![]() 均成立.
均成立.
(3)在(2)的条件下,若二次函数![]() 的象经过(-5,0),且在实数范围内,对于x的同一个值,这三个函数所对应的函数值
的象经过(-5,0),且在实数范围内,对于x的同一个值,这三个函数所对应的函数值![]() 均成立,求二次函数
均成立,求二次函数![]() 的解析式.
的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,抛物线![]() 交
交![]() 轴于
轴于![]() 两点(
两点(![]() 点在
点在![]() 点的左侧),交
点的左侧),交![]() 轴于点
轴于点![]() .已知
.已知![]() .
.
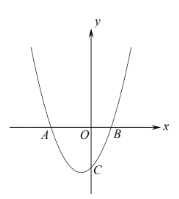
(1)求抛物线的解析式;
(2)已知直线![]() ,若直线与抛物线有且只有一个交点
,若直线与抛物线有且只有一个交点![]() 求
求![]() 的面积;
的面积;
(3)在(2)的条件下,抛物线上是否存在点![]() 使
使![]() 若存在,请直接写出点
若存在,请直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明家的门框上装有一把防盗门锁(如图1),其平面结构图如图2所示,锁身可以看成由两条等弧![]() ,
,![]() 和矩形
和矩形![]() 组成的,
组成的,![]() 的圆心是倒锁按钮点
的圆心是倒锁按钮点![]() .已知
.已知![]() 的弓形高
的弓形高![]() ,
,![]() ,
,![]() .当锁柄
.当锁柄![]() 绕着点
绕着点![]() 顺时针旋转至
顺时针旋转至![]() 位置时,门锁打开,此时直线
位置时,门锁打开,此时直线![]() 与
与![]() 所在的圆相切,且
所在的圆相切,且![]() ,
,![]() .
.
(1)求![]() 所在圆的半径;
所在圆的半径;
(2)求线段![]() 的长度.(
的长度.(![]() ,结果精确到
,结果精确到![]() )
)

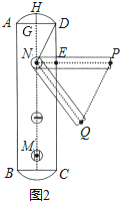
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com