A
分析:由DA=DB,GB=GC,利用等边对等角得到两对角相等,再根据AD为角平分线,得到一对角相等,等量代换可得∠BAD=∠B=∠GCB=∠CAD,由∠CAD=∠B,加上一对公共角相等可得△ACD∽△BCA;由∠AHG为三角形ACH的外角,利用外角性质得到∠AHG=∠ACH+∠DAC,由∠ACD=∠ACH+∠GCB,可得出∠AHG=∠ACD,再由∠BAD=∠B,可得△AHG∽△ACB;由对顶角相等可得∠CHD=∠AHG,再由∠AHG=∠ACD等量代换可得∠CHD与∠ACD相等,再加上∠B=∠GCB,可得出△CDH∽△BAC;而三角形ABD与三角形ABC不满足相似的条件,进而确定出正确的选项.
解答:∵DA=DB,GB=GC,
∴∠BAD=∠B,∠B=∠GCB,
又AD平分∠BAC,∴∠BAD=∠CAD,
∴∠BAD=∠B=∠GCB=∠CAD,
∴∠CAD=∠B,又∠ACD=∠CBA(公共角),
∴△ACD∽△BCA;
∵∠AHG为△DHC的外角,
∴∠AHG=∠ACH+∠DAC,
又∠ACD=∠ACH+∠GCB,且∠DAC=∠GCB,
∴∠AHG=∠ACD,又∠BAD=∠B,
∴△AHG∽△ACB;
∵∠CHD=∠AHG(对顶角相等),且∠AHG=∠ACD,
∴∠CHD=∠ACD,又∠B=∠GCB,
∴△CDH∽△BAC;
而∠B=∠B,∠BAD不等于∠ACB,则△ABD不相似△ABC,
则题中△ACD∽△BCA;△AHG∽△ACB;△CDH∽△BAC.
故选A.
点评:此题考查了相似三角形的判定,等腰三角形的性质,三角形外角性质,利用了转化及等量代换的数学思想,其中相似三角形的判定方法为:两对对应角相等的两三角形相似;两边对应成比例且夹角相等的两三角形相似;三边对应成比例的两三角形相似.

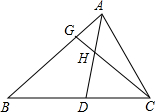 如图,在△ABC中,点D、G分别在BC、AB边上,AD与CG相交H,如果DA=DB,GB=GC,AD平分∠BAC,那么下列三角形中不与△ABC相似的是
如图,在△ABC中,点D、G分别在BC、AB边上,AD与CG相交H,如果DA=DB,GB=GC,AD平分∠BAC,那么下列三角形中不与△ABC相似的是

 阅读快车系列答案
阅读快车系列答案 如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为
如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为