
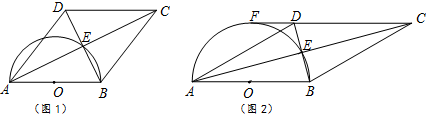
分析 (1)首先利用对角线互相平分的四边形是平行四边形得出四边形ABCD是平行四边形,进而利用菱形的判定方法得出答案;
(2)①首先求出△ABD的面积进而得出S△OBE=$\frac{1}{4}$S△ABD;
②首先求出扇形AOE的圆心角,进而利用扇形面积求出答案.
解答  (1)证明:∵AE=EC,BE=ED,
(1)证明:∵AE=EC,BE=ED,
∴四边形ABCD是平行四边形,
∵AB为直径,且过点E,
∴∠AEB=90°,即AC⊥BD,
∵四边形ABCD是平行四边形,
∴四边形ABCD是菱形;
(2)解:①连结OF,
∵DC的延长线于半圆相切于点F,
∴OF⊥CF,
∵FC∥AB,
∴OF即为△ABD中AB边上的高,
∴S△ABD=$\frac{1}{2}$AB×OF=$\frac{1}{2}$×8×4=16,
∵点O是AB中点,点E是BD的中点,
∴S△OBE=$\frac{1}{4}$S△ABD=4;
②过点D作DH⊥AB于点H,
∵AB∥CD,OF⊥CF,
∴FO⊥AB,
∴∠F=∠FOB=∠DHO=90°,
∴四边形OHDF为矩形,即DH=OF=4,
∵在Rt△DAH中,sin∠DAB=$\frac{DH}{AD}$=$\frac{1}{2}$,
∴∠DAH=30°,
∵D点O,E分别为AB,BD中点,
∴OE∥AD,
∴∠EOB=∠DAH=30°,
∴∠AOE=180°-∠EOB=150°,
∴S扇形AOE=$\frac{150π×{4}^{2}}{360}$=$\frac{20}{3}$π.
点评 此题主要考查了圆的综合以及菱形、矩形的判定方法、扇形面积求法等知识,正确掌握菱形的判定与性质是解题关键.


 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
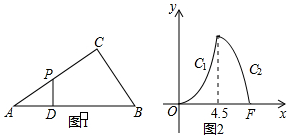 如图1,在Rt△ABC中,∠C=Rt∠,∠A=30°,D为AB上一个动点,过点D作DP⊥AB交折线A-C-B于点P,设AD的长为x,△APD的面积为y,y关于x的函数图象由C1,C2两段组成,如图2所示.
如图1,在Rt△ABC中,∠C=Rt∠,∠A=30°,D为AB上一个动点,过点D作DP⊥AB交折线A-C-B于点P,设AD的长为x,△APD的面积为y,y关于x的函数图象由C1,C2两段组成,如图2所示.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3 | B. | -1 | C. | 3或-1 | D. | -3或1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
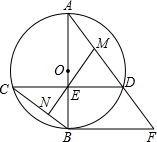 如图,AB为⊙O直径,且弦CD⊥AB于点E,过点B作⊙O的切线与AD的延长线交于点F.
如图,AB为⊙O直径,且弦CD⊥AB于点E,过点B作⊙O的切线与AD的延长线交于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
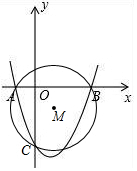 如图,抛物线y=x2-2x-3与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C.⊙M过A、B、C三点,P是抛物线上一点,连接PA,当PA与⊙M相切时,求点P的坐标.
如图,抛物线y=x2-2x-3与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C.⊙M过A、B、C三点,P是抛物线上一点,连接PA,当PA与⊙M相切时,求点P的坐标.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 时间x(天) | 每台空调的成本P(元) |
| 0<x≤5 | P=400 |
| 5<x≤12 | P=40x+200 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. |  | B. |  | C. | 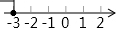 | D. | 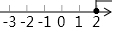 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
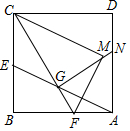 在正方形ABCD中,AB=2$\sqrt{5}$+2,E是边BC的中点,F是AB上一点,线段AE、CF交于点G,且CE=EG,将△CBF沿CF翻折,使得点B落在点M,连接GM并延长交AD于点N,则△AGN的面积为$\frac{16}{5}$$\sqrt{5}$.
在正方形ABCD中,AB=2$\sqrt{5}$+2,E是边BC的中点,F是AB上一点,线段AE、CF交于点G,且CE=EG,将△CBF沿CF翻折,使得点B落在点M,连接GM并延长交AD于点N,则△AGN的面积为$\frac{16}{5}$$\sqrt{5}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com