
【题目】如图1,已知![]() ,
, ![]() 与
与![]() 互余,
互余, ![]() 平分
平分![]() .
.
(1)在图1中,若![]() ,则
,则![]() ______
______![]() ,
, ![]() ______
______![]() .
.
(2)在图1中,设![]() ,
, ![]() ,请探究
,请探究![]() 与
与![]() 之间的数量关系(必须写出推理的主要过程,但每一步后面不必写出理由);
之间的数量关系(必须写出推理的主要过程,但每一步后面不必写出理由);
(3)在已知条件不变的前提下,当![]() 绕着点O顺时针转动到如图2的位置,此时
绕着点O顺时针转动到如图2的位置,此时![]() 与
与![]() 之间的数量关系是否还成立?若成立,请说明理由;若不成立,请直接写出此时
之间的数量关系是否还成立?若成立,请说明理由;若不成立,请直接写出此时![]() 与
与![]() 之间的数量关系.
之间的数量关系.

科目:初中数学 来源: 题型:
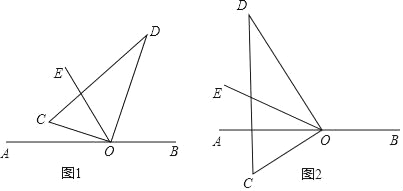
【题目】如图,直角三角板的直角顶点O在直线AB上,OC,OD是三角板的两条直角边,OE平分∠AOD.
(1)若∠COE=20°,则∠BOD= ;若∠COE=α,则∠BOD= (用含α的代数式表示)
(2)当三角板绕O逆时针旋转到图2的位置时,其它条件不变,试猜测∠COE与∠BOD之间有怎样的数量关系?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某探测队在地面A、B两处均探测出建筑物下方C处有生命迹象,已知探测线与地面的夹角分别是25°和60°,且AB=4米,求该生命迹象所在位置C的深度.(结果精确到1米.参考数据:sin25°≈0.4,cos25°≈0.9,tan25°≈0.5,![]() ≈1.7)
≈1.7)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中,AB=AC.

(1)试用直尺和圆规在AC上找一点D,使AD=BD(不写作法,但需保留作图痕迹).
(2)在(1)中,连接BD,若BD=BC,求∠A的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形ABCD中,AB=CD,M、N分别是AD和BC的中点,延长BA和CD分别交射线NM于点E和点F,若tan∠F=![]() , FC=FN,EN=
, FC=FN,EN=![]() , 则EF=
, 则EF= 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x、y的多项式(m﹣2)![]() +(n+3)xy2+3xy﹣5.
+(n+3)xy2+3xy﹣5.
(1)若原多项式是五次多项式,求m、n的值;
(2)若原多项式是五次四项式,求m、n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知顶点为(﹣3,﹣6)的抛物线y=ax2+bx+c经过点A,点(﹣2,m)和(﹣5,n)在该抛物线上,则下列结论中不正确的是( )
A.![]() >4ac
>4ac
B.m>n
C.方程a![]() +bx+c=﹣4的两根为﹣5或﹣1
+bx+c=﹣4的两根为﹣5或﹣1
D.a![]() +bx+c≥﹣6
+bx+c≥﹣6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明是个爱探究的学生,在学习完等腰三角形的判定定理之后,对于等腰![]() (如图甲),若
(如图甲),若![]() ,
,![]() ,小明发现,只要作
,小明发现,只要作![]() 的平分线就可以将
的平分线就可以将![]() 分成两个等腰三角形.
分成两个等腰三角形.
(1)你认为小明的发现正确吗?若正确,请给出证明过程;若不正确,请说明理由;
(2)请你对图乙的三角形进行探索,将![]() 分成两个等腰三角形,并写出顶角度数;
分成两个等腰三角形,并写出顶角度数;
(3)请你对图丙的三角形进行再探索,将![]() 分成三个等腰三角形,并写出顶角度数.
分成三个等腰三角形,并写出顶角度数.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A、B是直线m上两个定点,C是直线n上一个动点,且m∥n.以下说法:
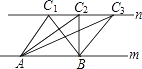
①△ABC的周长不变;
②△ABC的面积不变;
③△ABC中,AB边上的中线长不变.
④∠C的度数不变;
⑤点C到直线m的距离不变.
其中正确的有________(填序号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com