
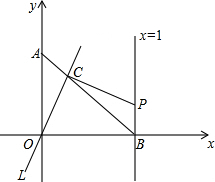
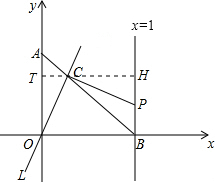
 ��ͼ����A��y���ϣ���B��x���ϣ���OA=OB=1������ԭ��O��ֱ��l���߶�AB�ڵ�C����C��OC�Ĵ��ߣ���ֱ��x=1�ཻ�ڵ�P���ֽ�ֱ��L��O����ת��ʹ����C��A��B�˶�����C������ڵ�һ�����ڣ�����AC�ij�Ϊt��������ͼ��������������̽����
��ͼ����A��y���ϣ���B��x���ϣ���OA=OB=1������ԭ��O��ֱ��l���߶�AB�ڵ�C����C��OC�Ĵ��ߣ���ֱ��x=1�ཻ�ڵ�P���ֽ�ֱ��L��O����ת��ʹ����C��A��B�˶�����C������ڵ�һ�����ڣ�����AC�ij�Ϊt��������ͼ��������������̽����| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |


 ������ȫ��������ϵ�д�
������ȫ��������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
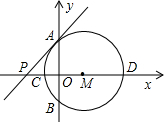 x1��0����D��x2��0�����㣬��x1��x2����x1��x2�Ƿ���x��2x+1��=��x+2��2��������
x1��0����D��x2��0�����㣬��x1��x2����x1��x2�Ƿ���x��2x+1��=��x+2��2���������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��ͼ����P��y���ϣ���P��x����A��B���㣬����BP���ӳ�����P��C������C��ֱ��y=2x+b��x����D���ҡ�P�İ뾶Ϊ
��ͼ����P��y���ϣ���P��x����A��B���㣬����BP���ӳ�����P��C������C��ֱ��y=2x+b��x����D���ҡ�P�İ뾶Ϊ| 5 |
| k |
| x |
| A����4 | ||
| B��-4 | ||
C��-2
| ||
| D��4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
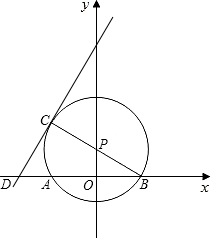 ��ֱ��y=2x+b��x����D���ҡ�P�İ뾶Ϊ
��ֱ��y=2x+b��x����D���ҡ�P�İ뾶Ϊ| 5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
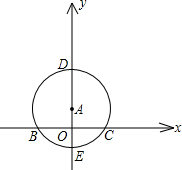 -1��
-1���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ���ڵ�D��˳������I��D��B���������ɵȱ������Σ���A��B�����������y=ax2+bx+c�Ķ���PҲ�ڰ�ԲI�ϣ�
���ڵ�D��˳������I��D��B���������ɵȱ������Σ���A��B�����������y=ax2+bx+c�Ķ���PҲ�ڰ�ԲI�ϣ��鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com