
【题目】如图,将矩形ABCD绕点A顺时针旋转到矩形AB′C′D′的位置,旋转角为α(0°<α<90°).若∠1=112°,则∠α的大小是( ) 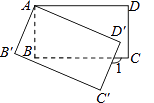
A.68°
B.20°
C.28°
D.22°
科目:初中数学 来源: 题型:
【题目】现有一根长为1米的木杆,第1次截取其长度的一半,第2次截取其第1次剩下长度的一半,第3次截取其第2次剩下长度的一半,如此反复截取,则第n(n为正整数)次截取后,此木杆剩下的长度为米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列等式:
第1个等式:a1=![]() =
=![]() ﹣
﹣![]() ;
;
第2个等式:a2=![]() =
=![]() ﹣
﹣![]() ;
;
第3个等式:a3=![]() =
=![]() ﹣
﹣![]() ;
;
第4个等式:a4=![]() =
=![]() ﹣
﹣![]() .
.
按上述规律,回答以下问题:
(1)用含n的代数式表示第n个等式:an=_____=_____;
(2)式子a1+a2+a3+…+a20=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国庆期间,为了满足百姓的消费需求,某商店计划用170000元购进一批家电,这批家电的进价和售价如表:
类别 | 彩电 | 冰箱 | 洗衣机 |
进价(元/台) | 2000 | 1600 | 1000 |
售价(元/台) | 2300 | 1800 | 1100 |
若在现有资金允许的范围内,购买表中三类家电共100台,其中彩电台数是冰箱台数的2倍,设该商店购买冰箱x台.
(1)商店至多可以购买冰箱多少台?
(2)购买冰箱多少台时,能使商店销售完这批家电后获得的利润最大?最大利润为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点O为直线AB上一点,过点O作射线OC,使∠BOC=65°.将一直角三角板的直角顶点放在点O处.
(1)如图①,将三角板MON的一边ON与射线OB重合时,则∠MOC= ;
(2)如图②,将三角板MON绕点O逆时针旋转一定角度,此时OC是∠MOB的角平分线,求旋转角∠BON= ;∠CON= .
(3)将三角板MON绕点O逆时针旋转至图③时,∠NOC=5°,求∠AOM.
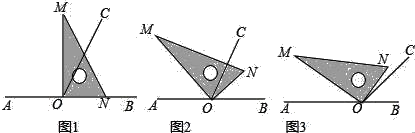
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠B=∠D=90°,∠BAD=105°,在BC,CD上分别找一点M、N,使得△AMN周长最小,则∠AMN+∠ANM的度数为 ( )

A. 100° B. 105° C. 120° D. 150°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,点O是直线AB上的一点,∠COD是直角,OE平分∠BOC.
(1)如图①,若∠AOC=40°,求∠DOE的度数;
(2)如图①,若∠AOC=α,直接写出∠DOE的度数(用含α的代数式表示)
(3)将图①中的∠COD绕顶点O顺时针旋转至图②的位置,OE平分∠BOC.
①探究∠AOC和∠DOE的度数之间的关系,写出你的结论,并说明理由;
②在∠AOC的内部有一条射线OF,且∠AOC﹣3∠AOF=2∠BOE,试确定∠AOF与∠DOE的度数之间的关系,说明理由.
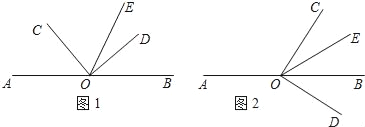
查看答案和解析>>
科目:初中数学 来源: 题型:
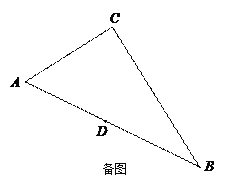
【题目】已知,如图,在Rt△ABC中,∠C=90°,∠A=60°,AC=3,点D为AB的中点,点E为线段BC上的点,连接DE,把△BDE沿着DE翻折得△B1DE.
(1)当A、D、B1、C构成的四边形为平行四边形,求DE的长;
(2)当DB1⊥AC时,求△DE B1和△ABC重叠部分的面积.
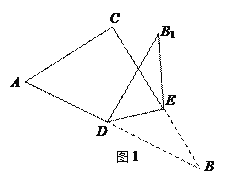


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一般情况下![]() 不成立,但有些数可以使得它成立,例如:m=n=0时,我们称使得
不成立,但有些数可以使得它成立,例如:m=n=0时,我们称使得![]() 成立的一对数m,n为“相伴数对”,记为(m,n).
成立的一对数m,n为“相伴数对”,记为(m,n).
(1)若(m,1)是“相伴数对”,则m=_____;
(2)(m,n)是“相伴数对”,则代数式![]() m﹣[n+
m﹣[n+![]() (6﹣12n﹣15m)]的值为_____.
(6﹣12n﹣15m)]的值为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com