(1)证明:显然,BE∥GF,
根据对称性得∠1=∠2,∠3=∠4
∵A1D1∥B1C1
∴∠1+∠2=∠3+∠4
∴∠1=∠2=∠3=∠4
∴EF∥BG
∴四边形BEFG是平行四边形;
(2)解:△B1BG是直角三角形,
理由:
∵A1D1∥B1C1
∴∠4=∠6
∴∠3=∠6
∴BF=FG
∵B1F与BF关于EF对称
∴B1F=BF
∴B1F=BF=FG
∴△B1BG是直角三角形.
分析:(1)本题的关键是证EF∥GB,可根据平行线A1D1,B1C1以及折叠的性质,来得出∠2=∠3,从而求出EF∥BG;
(2)应该是直角三角形,根据直角三角形的判定,如果得出B1F=BF=FG即可得出三角形B1BG是直角三角形,根据折叠的性质,B1F=BF,关键是证BF=FG,可根据(1)中∠3=∠4,以及A1D1∥B1C1,来求出∠3=∠6,进而求出FB=FG.
点评:此题主要考查图形的折叠问题,折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,只是位置变化.

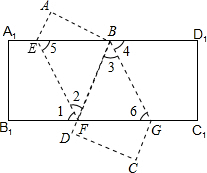 如图,矩形A1BlC1D1沿EF折叠,使B1点落在A1D1边上的B处;沿BG折叠,使D1点落在D处且BD过F点.
如图,矩形A1BlC1D1沿EF折叠,使B1点落在A1D1边上的B处;沿BG折叠,使D1点落在D处且BD过F点.

 灵星计算小达人系列答案
灵星计算小达人系列答案