
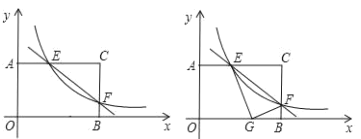
【题目】矩形AOBC中,OB=4,OA=3.分别以OB、OA所在直线为x轴、y轴,建立如图1所示的平面直角坐标系.F是BC边上一个动点(不与B、C重合).过点F的反比例函数y=![]() (k>0)的图象与边AC交于点E.
(k>0)的图象与边AC交于点E.
(1)当点F运动到边BC的中点时,点E的坐标为__________;
(2)连接EF,求∠EFC的正切值;
(3)如图2,将△CEF沿EF折叠,点C恰好落在边OB上的点G处,求BG的长度.
【答案】(1)E(2,3);(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)先确定出点C坐标,进而得出点F坐标,即可求出反比例函数解析式,再根据E点纵坐标为3即可确定E点坐标;
(2)先确定出点F的横坐标,进而表示出点F的坐标,得出CF,同理表示出CE,即可得出结论;
(3)过点E作EH⊥OB于H,先判断出△EHG∽△GBF,根据相似三角形对应边成比例即可求出BG.
解:(1)∵OA=3,OB=4,
∴B(4,0),C(4,3),
∵F是BC的中点,
![]() ,
,
∵F在反比例![]() 函数图象上,
函数图象上,
![]() ,
,
∴反比例函数的解析式为![]() ,
,
∵E点的纵坐标为3,
∴E(2,3);
(2)∵F点的横坐标为4,
![]()
![]() ,
,
∵E的纵坐标为3,
![]()
![]()
在Rt△CEF中,![]() ;
;
(3)如图,由(2)知,![]() ,
,
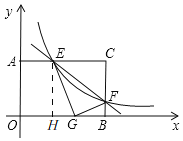
过点E作EH⊥OB于H,
∴EH=OA=3,∠EHG=∠GBF=90°,
∴∠EGH+∠HEG=90°,
由折叠知,![]() ,
,![]() ,∠EGF=∠C=90°,
,∠EGF=∠C=90°,
∴∠EGH+∠BGF=90°,
∴∠HEG=∠BGF,
∵∠EHG=∠GBF=90°,
∴△EHG∽△GBF,
![]() ,
,
![]() ,即
,即![]() .
.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】某出租公司有若干辆同一型号的货车对外出租,每辆货车的日租金实行淡季、旺季两种价格标准,旺季每辆货车的日租金比淡季上涨![]() .据统计,淡季该公司平均每天有
.据统计,淡季该公司平均每天有![]() 辆货车未出租,日租金总收入为
辆货车未出租,日租金总收入为![]() 元;旺季所有的货车每天能全部租出,日租金总收入为
元;旺季所有的货车每天能全部租出,日租金总收入为![]() 元.
元.
(1)该出租公司这批对外出租的货车共有多少辆?淡季每辆货车的日租金多少元?
(2)经市场调查发现,在旺季如果每辆货车的日租金每上涨![]() 元,每天租出去的货车就会减少
元,每天租出去的货车就会减少![]() 辆,不考虑其它因素,每辆货车的日租金上涨多少元时,该出租公司的日租金总收入最高?
辆,不考虑其它因素,每辆货车的日租金上涨多少元时,该出租公司的日租金总收入最高?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD外取一点E,连接AE、BE、DE.过点A作AE的垂线交DE于点P.若AE=AP=1,PB=![]() .下列结论:①△APD≌△AEB;②点B到直线AE的距离为
.下列结论:①△APD≌△AEB;②点B到直线AE的距离为![]() ;③EB⊥ED;④S△APD+S△APB=1+
;③EB⊥ED;④S△APD+S△APB=1+![]() ;⑤S正方形ABCD=4+
;⑤S正方形ABCD=4+![]() .其中正确结论的序号是 .
.其中正确结论的序号是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
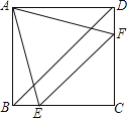
【题目】如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E,F分别在BC和CD上,下列结论:①CE=CF;②BD=1+![]() ;③BE+DF=EF;④∠AEB=75°.其中正确的序号是______.
;③BE+DF=EF;④∠AEB=75°.其中正确的序号是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将函数y=![]() (x﹣2)2+1的图象沿y轴向上平移得到一条新函数的图象,其中点A(1,m),B(4,n)平移后的对应点分别为点A'、B'.若曲线段AB扫过的面积为9(图中的阴影部分),则新图象的函数表达式是( )
(x﹣2)2+1的图象沿y轴向上平移得到一条新函数的图象,其中点A(1,m),B(4,n)平移后的对应点分别为点A'、B'.若曲线段AB扫过的面积为9(图中的阴影部分),则新图象的函数表达式是( )

A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,已知点A(-1,0), B(0,![]() ),对△OAB连续作旋转变换,依次得到△1,△2,△3,△4,…,则△2019的直角顶点的坐标为______________.
),对△OAB连续作旋转变换,依次得到△1,△2,△3,△4,…,则△2019的直角顶点的坐标为______________.

查看答案和解析>>
科目:初中数学 来源: 题型:
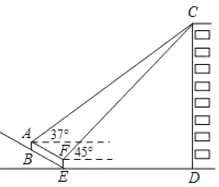
【题目】我校数学兴趣小组的同学要测量建筑物![]() 的高度,如图,建筑物
的高度,如图,建筑物![]() 前有一段坡度为
前有一段坡度为![]() 的斜坡
的斜坡![]() ,小明同学站在斜坡上的
,小明同学站在斜坡上的![]() 点处,用测角仪测得建筑物屋顶
点处,用测角仪测得建筑物屋顶![]() 的仰角为
的仰角为![]() ,接着小明又向下走了
,接着小明又向下走了![]() 米,刚好到达坡底
米,刚好到达坡底![]() 处,这时测到建筑物屋顶
处,这时测到建筑物屋顶![]() 的仰角为
的仰角为![]() ,
,![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 在同一平面内.若测角仪的高度
在同一平面内.若测角仪的高度![]() 米,则建筑物
米,则建筑物![]() 的高度约为( ).(精确到0.1米,参考数据:
的高度约为( ).(精确到0.1米,参考数据:![]() ,
,![]() ,
,![]() )
)
A.38.6B.39.0C.40.0D.41.5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com