
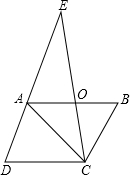
 如图,△ABC中,∠B=58°,AB∥CD,∠ADC=∠DAC,∠ACB的平分线交DA的延长线于点E,则∠E的度数为29°.
如图,△ABC中,∠B=58°,AB∥CD,∠ADC=∠DAC,∠ACB的平分线交DA的延长线于点E,则∠E的度数为29°. 分析 根据平行线的性质得到∠EAB=∠D,设∠EAB=∠ADC=∠DAC=α,∠ACO=∠BCO=β,根据三角形的内角和得到∠ACD=180°-2α,由平行线的性质得到∠BAC=∠ACD,∠B+∠DCB=180°,根据三角形的内角和即可得到结论.
解答 解:∵AB∥CD,
∴∠EAB=∠D,
∵∠ADC=∠DAC,
∴∠EAB=∠ADC=∠DAC,
∵CE平分∠ACB,
∴∠ACO=∠BCO,
设∠EAB=∠ADC=∠DAC=α,∠ACO=∠BCO=β,
∴∠ACD=180°-2α,
∵AB∥CD,
∴∠BAC=∠ACD,∠B+∠DCB=180°,
∴180°-2α+2β+58°=180°,
∴α=β+29°
∴∠E=180°-∠EAC-∠ACE=180°-α-(180°-2α)-β=α-β=β+29°-β=29°.
故答案为:29°.
点评 本题考查了平行线的性质,三角形的内角和,角平分线的定义,熟练掌握平行线的性质是解题的关键.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:解答题
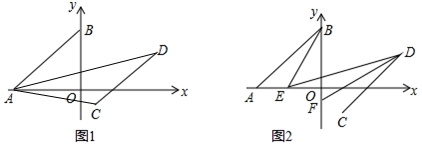
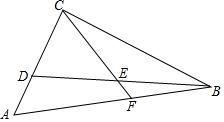 已知:如图,在Rt△ABC中,∠ACB=90°,点D在边AC上,点E是BD的中点,CE的延长线交边AB于点F,且∠CED=∠A.
已知:如图,在Rt△ABC中,∠ACB=90°,点D在边AC上,点E是BD的中点,CE的延长线交边AB于点F,且∠CED=∠A.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
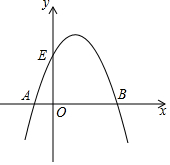 已知抛物线经过点A(-1,0),B(3,0),C(1,4),与y轴交于点E.
已知抛物线经过点A(-1,0),B(3,0),C(1,4),与y轴交于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
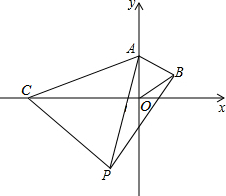 如图,等边△AOB中点O是原点,点A在y轴上,点B的坐标是(2$\sqrt{3}$,2),小明做一个数学实验,在x轴上取一动点C,以AC为一边画出等边△ACP,移动点C时,探究点P的位置变化情况.
如图,等边△AOB中点O是原点,点A在y轴上,点B的坐标是(2$\sqrt{3}$,2),小明做一个数学实验,在x轴上取一动点C,以AC为一边画出等边△ACP,移动点C时,探究点P的位置变化情况.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
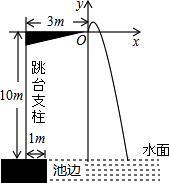 如图,2016年里约奥运会上,某运动员在10米跳台跳水比赛时估测身体(看成一点)在空中的运动路线是抛物线y=-$\frac{25}{6}$x2+$\frac{10}{3}$x(图中标出的数据为已知条件),运动员在空中运动的最大高度离水面为$10\frac{2}{3}$米.
如图,2016年里约奥运会上,某运动员在10米跳台跳水比赛时估测身体(看成一点)在空中的运动路线是抛物线y=-$\frac{25}{6}$x2+$\frac{10}{3}$x(图中标出的数据为已知条件),运动员在空中运动的最大高度离水面为$10\frac{2}{3}$米.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3$\sqrt{3}$×5$\sqrt{3}$=15$\sqrt{3}$ | B. | 3$\sqrt{2}$$+2\sqrt{3}$=5$\sqrt{6}$ | C. | $\sqrt{8}$$-\sqrt{6}$=$\sqrt{2}$ | D. | $\sqrt{60}$$÷\sqrt{5}$=2$\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com