
【题目】如图,直线MN与x轴、y轴分别交于A、C两点,分别过A、C两点作x轴、y轴的垂线相交于B点,且OA、OC(OA>OC)的长分别是一元二次方程x2﹣14x+48=0的两个实数根.

(1)求A、C两点的坐标.
(2)求直线MN的表达式.
(3)在直线MN上存在点P,使以点P、B、C三点为顶点的三角形是等腰三角形,请直接写出P点的坐标.
【答案】(1) A(8,0),C(0,6);(2) y=﹣![]() x+6;;(3) P点的坐标为(4,3)或(﹣
x+6;;(3) P点的坐标为(4,3)或(﹣![]() ,
,![]() )或(
)或(![]() ,
,![]() )或(
)或(![]() ,﹣
,﹣![]() )
)
【解析】
(1)通过解方程x2-14x+48=0可以求得OC=6,OA=8.即可得出答案;
(2)设直线MN的解析式是y=kx+b(k≠0).把点A、C的坐标分别代入解析式,列出关于系数k、b的方程组,通过解方程组即可求得它们的值;
(3)需要分类讨论:①当PC=PB时;②当PC=BC时;③当PB=BC时;根据等腰三角形的性质、两点间的距离公式以及一次函数图象上点的坐标特征进行解答.
(1)∵x2﹣14x+48=0,
解得:x1=6,x2=8.
∵OA,OC(OA>OC)的长分别是一元二次方程x2﹣14x+48=0的两个实数根,
∴OC=6,OA=8.
∴A(8,0),C(0,6);
(2)设直线MN的解析式是y=kx+b(k≠0).
由(1)知,A(8,0),C(0,6),
∵点A、C都在直线MN上,
∴![]() ,
,
解得: ,
,
∴直线MN的解析式为y=﹣![]() x+6;
x+6;
(3)∵A(8,0),C(0,6),过A、C两点作x轴、y轴的垂线相交于B点,
∴B(8,6).
∵点P在直线MNy=﹣![]() x+6上,
x+6上,
∴设P(a,﹣![]() a+6),
a+6),
当以点P,B,C三点为顶点的三角形是等腰三角形时,分三种情况讨论:如图所示:

①当PC=PB时,点P是线段BC的中垂线与直线MN的交点,则P(4,3);
②当PC=BC时,a2+(﹣![]() a+6﹣6)2=82,
a+6﹣6)2=82,
解得:a=±![]() ,
,
则P(﹣![]() ,
,![]() )或(
)或(![]() ,
,![]() );
);
③当PB=BC时,(a﹣8)2+(![]() a﹣6+6)2=64,
a﹣6+6)2=64,
解得:a=![]() ,
,
则﹣![]() a+6=﹣
a+6=﹣![]() ,
,
∴P(![]() ,﹣
,﹣![]() ).
).
综上所述,P点的坐标为(4,3)或(﹣![]() ,
,![]() )或(
)或(![]() ,
,![]() )或(
)或(![]() ,﹣
,﹣![]() ).
).


科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A(3,0),B(﹣1,0)两点,与y轴相交于点C(0,﹣3)
(1)求该二次函数的解析式;
(2)设E是y轴右侧抛物线上异于点A的一个动点,过点E作x轴的平行线交抛物线于另一点F,过点F作FG垂直于x轴于点G,再过点E作EH垂直于x轴于点H,得到矩形EFGH,则在点E的运动过程中,当矩形EFGH为正方形时,求出该正方形的边长;
(3)设P点是x轴下方的抛物线上的一个动点,连接PA、PC,求△PAC面积的取值范围,若△PAC面积为整数时,这样的△PAC有几个?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数y=![]() 的图象与一次函数y=kx+b的图象交于A,B两点,
的图象与一次函数y=kx+b的图象交于A,B两点,
点A的坐标为(2,6),点B的坐标为(n,1).
(1)求反比例函数与一次函数的表达式;

(2)点E为y轴上一个动点,若S△AEB=10,求点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的布袋里装有4个大小、质地均相同的乒乓球,每个球上面分别标有1,2,3,4.小林先从布袋中随机抽取一个乒乓球(不放回去),再从剩下的3个球中随机抽取第二个乒乓球.
(1)请你用树状图或列表法列出所有可能的结果;
(2)求两次取得乒乓球的数字之积为奇数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
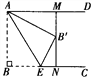
【题目】如图,已知AD∥BC,AB⊥BC,AB=3.点E为射线 BC上一个动点,连接AE,将△ABE沿AE折叠,点B落在点B′处,过点B′作AD的垂线,分别交AD,BC于点M,N.当点B′为线段MN的三等分点时,BE的长为__________ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△PAB中,M.N是AB上两点,△PMN是等边三角形,∠APM=∠B.
(1)求证:∠A=∠BPN;
(2)求证:MN2=AM·BN;
(3)若AP=![]() ,AM=1,求线段MN,PB的长.
,AM=1,求线段MN,PB的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的布袋中有分别标有汉字“我”、“的”、“祖”、“国”的四个小球,除汉字外没有任何区别,每次摸球前先摇匀再摸球.
(1)若从中任意摸一个球,求摸出球上的汉字刚好是“国”字的概率;
(2)小林从中任取一个球,记下汉字后放回,摇匀后再从中任取一个.请用树状图或列表法,求小林取出的两个球上的汉字恰好能组成“祖国”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=a(x﹣3)2+![]() 过点C(0,4),顶点为M,与x轴交于A、B两点.如图所示以AB为直径作圆,记作⊙D,下列结论:①抛物线的对称轴是直线x=3;②点C在⊙D外;③在抛物线上存在一点E,能使四边形ADEC为平行四边形;④直线CM与⊙D相切.正确的结论是( )
过点C(0,4),顶点为M,与x轴交于A、B两点.如图所示以AB为直径作圆,记作⊙D,下列结论:①抛物线的对称轴是直线x=3;②点C在⊙D外;③在抛物线上存在一点E,能使四边形ADEC为平行四边形;④直线CM与⊙D相切.正确的结论是( )

A.①③B.①④C.①③④D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是正方形,![]() ,AC、BD交于点O,点P、Q分别是AB、BD上的动点,点P的运动路径是
,AC、BD交于点O,点P、Q分别是AB、BD上的动点,点P的运动路径是![]() ,点Q的运动路径是BD,两点的运动速度相同并且同时结束.若点P的行程为x,
,点Q的运动路径是BD,两点的运动速度相同并且同时结束.若点P的行程为x,![]() 的面积为y,则y关于x的函数图象大致为( )
的面积为y,则y关于x的函数图象大致为( )

A.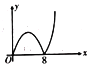 B.
B.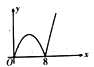 C.
C.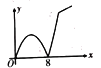 D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com