
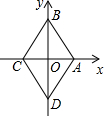
 菱形ABCD在直角坐标系中的位置如图所示,其中点A的坐标为(1,0),点B的坐标为(0,$\sqrt{3}$),动点P从点A出发,沿A→B→C→D→A→B→…的路径,在菱形的边上以每秒1个单位长度的速度移动,移动到第2015秒时,点P的坐标为( $\frac{3}{4}$,-$\frac{\sqrt{3}}{4}$).
菱形ABCD在直角坐标系中的位置如图所示,其中点A的坐标为(1,0),点B的坐标为(0,$\sqrt{3}$),动点P从点A出发,沿A→B→C→D→A→B→…的路径,在菱形的边上以每秒1个单位长度的速度移动,移动到第2015秒时,点P的坐标为( $\frac{3}{4}$,-$\frac{\sqrt{3}}{4}$). 分析 先根据勾股定理求出菱形的边长,再根据点P的运动速度求出沿A→B→C→D→A所需的时间,进而可得出结论.
解答 解:∵A(1,0),B(0,$\sqrt{3}$),
∴AB=$\sqrt{{1}^{2}+(\sqrt{3})^{2}}$=2.
∵点P的运动速度为0.5米/秒,
∴从点A到点B所需时间=$\frac{2}{0.5}$=4秒,
∴沿A→B→C→D→A所需的时间=4×4=16秒.
∵$\frac{2015}{16}$=125…15,
∴移动到第2015秒和第15秒的位置相同,当P运动到第15秒时,如图所示,作PE⊥AC于E,PF⊥OD于F.
可得 $\frac{AP}{AD}$=$\frac{1}{4}$,
∵PE∥OD,PF∥OA,
∴$\frac{PE}{OD}$=$\frac{AP}{AD}$,$\frac{PF}{OA}$=$\frac{DP}{DA}$,
∴PE=$\sqrt{3}$×$\frac{1}{4}$=$\frac{\sqrt{3}}{4}$,PF=1×$\frac{3}{4}$=$\frac{3}{4}$,
∴P( $\frac{3}{4}$,-$\frac{\sqrt{3}}{4}$).
故答案为:( $\frac{3}{4}$,-$\frac{\sqrt{3}}{4}$).
点评 本题考查的是菱形的性质,路程、速度、时间之间的关系,根据题意得出点P运动一周所需的时间是解答此题的关键,学会添加常用辅助线,利用平行线的性质解决问题,所以中考常考题型.


 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 路程(千米) | 运费(元/吨.千米) | |||
| 甲仓库 | 乙仓库 | 甲仓库 | 乙仓库 | |
| A地 | 25 | 20 | 1 | 0.8 |
| B地 | 20 | 15 | 1.2 | 1.2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在⊙O中,弦AC,BD相交于点M,且∠A=∠B
如图,在⊙O中,弦AC,BD相交于点M,且∠A=∠B查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com