
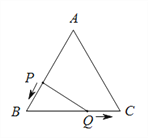
【题目】如图,已知△ABC是边长为3cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,它们的速度都是1 cm/s,当点P到达点B时,P、Q两点停止运动,设点P的运动时间为t(s),则(1)BP![]() cm,BQ
cm,BQ![]() cm.(用含t的代数式表示)
cm.(用含t的代数式表示)
(2)当t为何值时,△PBQ是直角三角形?
【答案】(1)3-t,t;(2)当t=1s或t=2s时,△PBQ是直角三角形.
【解析】分析:(1)根据路程=速度×时间即可求得;(2)根据等边三角形的性质可以知道这个直角三角形∠B=60°,所以就可以表示出BQ与PB的关系,要分情况进行讨论:①∠BPQ=90°;②∠PQB=90°.然后在直角三角形BQP中根据BP,BQ的表达式和∠B的度数进行求解即可.
本题解析:
(1)![]() cm,
cm,![]() cm
cm
在 △PBQ中,![]()
若△PBQ是直角三角形,则点P或点Q
为直角顶点
①若点P为直角顶点,因为![]() ,所以
,所以![]()
所以![]() 即t=2(3-t), 解得t=2
即t=2(3-t), 解得t=2
②若点Q是直角顶点,∵![]() ,∴
,∴![]()
∴![]() 即3-t=2t, 解得t=1
即3-t=2t, 解得t=1
答:当t=1s或t=2s时,△PBQ是直角三角形


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:初中数学 来源: 题型:
【题目】某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光明且温度为18![]() 的条件下生长最快的新品种.如图,是某天恒温系统从开启到关闭及关闭后,大棚内温度y(
的条件下生长最快的新品种.如图,是某天恒温系统从开启到关闭及关闭后,大棚内温度y(![]() )随时间x(小时)变化的函数图象,其中BC段足双曲线
)随时间x(小时)变化的函数图象,其中BC段足双曲线![]() 的一部分,请根据图中信息解答下列问题:
的一部分,请根据图中信息解答下列问题:

(1)恒温系统这天保持大棚内温度18![]() 的时间有多少小时?
的时间有多少小时?
(2)求k值;
(3)当x=15时,大棚内的温度约为多少度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察思考:如图, ![]() 、
、![]() 是直线
是直线![]() 上的两个定点,点
上的两个定点,点![]() 、
、![]() 在直线
在直线![]() 上运动(点
上运动(点![]() 在点
在点![]() 的左侧),
的左侧),![]() ,已知
,已知![]() ,
, ![]() 、
、![]() 间的距离为
间的距离为![]() ,连接
,连接![]() 、
、![]() 、
、![]() ,把
,把![]() 沿
沿![]() 折叠得
折叠得![]() .
.
(![]() )当
)当![]() 、
、![]() 两点重合时,则
两点重合时,则![]() __________
__________ ![]() .
.
(![]() )当
)当![]() 、
、![]() 两点不重合时,
两点不重合时,
①连接![]() ,探究
,探究![]() 与
与![]() 的位置关系,并说明理由.
的位置关系,并说明理由.
②若以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是矩形,画出示意图并直接写出
为顶点的四边形是矩形,画出示意图并直接写出![]() 的长.
的长.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图![]() 是一个可以自由转动的转盘,被分成了面积相等的三个扇形,分别标有数
是一个可以自由转动的转盘,被分成了面积相等的三个扇形,分别标有数![]() ,
, ![]() ,
, ![]() ,甲转动一次转盘,转盘停止后指针指向的扇形内的数记为
,甲转动一次转盘,转盘停止后指针指向的扇形内的数记为![]() (如果指针恰好指在分割线上,那么重转一次,直到指针指向某一扇形为止).图
(如果指针恰好指在分割线上,那么重转一次,直到指针指向某一扇形为止).图![]() 是背面完全一样、牌面数字分别是
是背面完全一样、牌面数字分别是![]() ,
, ![]() ,
, ![]() ,
, ![]() 的四张扑克牌,把四张扑克牌背面朝上,洗匀后放在桌面上,乙随机抽出一张牌的牌面数字记为
的四张扑克牌,把四张扑克牌背面朝上,洗匀后放在桌面上,乙随机抽出一张牌的牌面数字记为![]() .计算
.计算![]() 的值.
的值.


(![]() )用树状图或列表法求
)用树状图或列表法求![]() 的概率.
的概率.
(![]() )甲乙两人玩游戏,规定:当
)甲乙两人玩游戏,规定:当![]() 是正数时,甲胜;否则,乙胜,你认为这个游戏规则对甲乙双方公平吗?请说明理由.
是正数时,甲胜;否则,乙胜,你认为这个游戏规则对甲乙双方公平吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
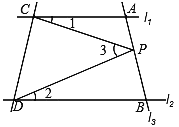
【题目】如图,已知直线l1∥l2,且l3和l1、l2分别交于A、B两点,点P在直线AB上.
(1)试说明∠1,∠2,∠3之间的关系式;(要求写出推理过程)
(2)如果点P在A、B两点之间(点P和A、B不重合)运动时,试探究∠1,∠2,∠3之间的关系是否发生变化?(只回答)
(3)如果点P在A、B两点外侧(点P和A、B不重合)运动时,试探究∠1,∠2,∠3之间的关系.(要求写出推理过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠A=60°,BD、CD分别平分∠ABC、∠ACB,M、N、Q分别在DB、DC、BC的延长线上,BE、CE分别平分∠MBC、∠BCN,BF、CF分别平分∠EBC、∠ECQ,则∠F=( ).

A. 60° B. 45° C. 30° D. 15°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,已知一次函数y=![]() x+1的图象与x轴,y轴分别交于A,B两点,以AB为边在第二象限内作正方形ABCD.
x+1的图象与x轴,y轴分别交于A,B两点,以AB为边在第二象限内作正方形ABCD.
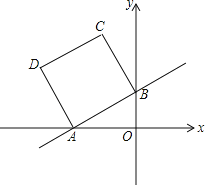
(1)求边AB的长;
(2)求点C,D的坐标;
(3)在x轴上是否存在点M,使△MDB的周长最小?若存在,请求出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:∠MON=80°,OE平分∠MON,点A、B、C分别是射线OM、OE、ON上的动点(A、B、C不与点O 重合),连接AC交射线OE于点D.设∠OAC=x°.
(1)如图1,若AB∥ON,则:①∠ABO的度数是 ;
②如图2,当∠BAD=∠ABD时,试求x的值(要说明理由);
(2)如图3,若AB⊥OM,则是否存在这样的X的值,使得△ADB中有两个相等的角?若存在,直接写出x的值;若不存在,说明理由.(自己画图)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com