

分析 分0≤t≤$\frac{1}{2}$、$\frac{1}{2}$<t≤1、1<t≤$\frac{3}{2}$、$\frac{3}{2}$<t≤2四种情况,根据三角形的面积公式和割补法列出重叠部分面积可得.
解答 解:∵边长都是1的正方形和正三角形,其一边在同一水平线上,三角形沿该水平线左向右匀速穿过正方形.设穿过的时间为t,正方形与三角形重合部分的面积为S,
∴S关于t的函数大致图象应为:三角形进入正方形以前是空白部分面积逐渐增大,
当0≤t≤$\frac{1}{2}$时,S=$\frac{1}{2}$×t×$\sqrt{3}$t=$\frac{\sqrt{3}}{2}$t2;
当$\frac{1}{2}$<t≤1时,S=$\frac{1}{2}$×1×$\frac{\sqrt{3}}{2}$-$\frac{1}{2}$×(1-t)×$\sqrt{3}$(1-t)=-$\frac{\sqrt{3}}{2}$t2+$\sqrt{3}$t-$\frac{\sqrt{3}}{4}$;
当1<t≤$\frac{3}{2}$时,S=$\frac{1}{2}$×1×$\frac{\sqrt{3}}{2}$-$\frac{1}{2}$×(t-1)×$\sqrt{3}$(t-1)=-$\frac{\sqrt{3}}{2}$t2+$\sqrt{3}$t-$\frac{\sqrt{3}}{4}$,
当$\frac{3}{2}$<t≤2时,S=$\frac{1}{2}$(2-t)×$\sqrt{3}$(2-t)=$\frac{\sqrt{3}}{2}$t2-2$\sqrt{3}$t+2$\sqrt{3}$.
点评 本题主要考查二次函数的应用,理解题意找到面积变化的拐点是解题的解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 95 90 | B. | 95 85 | C. | 90 95 | D. | 80 85 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
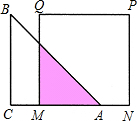 如图,等腰直角△ABC的直角边长与正方形MNPQ的边长均为10cm,AC与MN在同一直线上,开始时A点与M点重合,让向右运动,最后A点与N点重合,则重叠部分面积ycm2与MA长度xcm之间关系式y=$\frac{1}{2}$x2;自变量的取值范围是0<x≤10.
如图,等腰直角△ABC的直角边长与正方形MNPQ的边长均为10cm,AC与MN在同一直线上,开始时A点与M点重合,让向右运动,最后A点与N点重合,则重叠部分面积ycm2与MA长度xcm之间关系式y=$\frac{1}{2}$x2;自变量的取值范围是0<x≤10.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
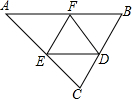 如图,在△ABC中,AB=6,AB边上的高为3,点F为AB上一点,点E为AC边上的一个动点,DE∥AB交BC于点D,若AB与DE之间的距离为x,则△DEF的面积y关于x的函数关系是3x-x2.
如图,在△ABC中,AB=6,AB边上的高为3,点F为AB上一点,点E为AC边上的一个动点,DE∥AB交BC于点D,若AB与DE之间的距离为x,则△DEF的面积y关于x的函数关系是3x-x2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
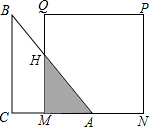 如图,已知等腰直角三角形ABC的直角边长与正方形MNPQ的边长均为20cm,AC与MN在同一条直线上,开始时点A与点N重合,让△ABC以2cm/s的速度向左运动,最终点A与点M重合.求:
如图,已知等腰直角三角形ABC的直角边长与正方形MNPQ的边长均为20cm,AC与MN在同一条直线上,开始时点A与点N重合,让△ABC以2cm/s的速度向左运动,最终点A与点M重合.求:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
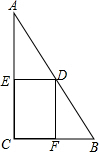 如图,在Rt△ABC中,已知∠C=90°,BC=4,AC=8,点D在斜边AB上,分别作DE⊥AC,DF⊥BC,垂足分别为E、F.得四边形DECF.设DE=x,DF=y
如图,在Rt△ABC中,已知∠C=90°,BC=4,AC=8,点D在斜边AB上,分别作DE⊥AC,DF⊥BC,垂足分别为E、F.得四边形DECF.设DE=x,DF=y查看答案和解析>>
科目:初中数学 来源: 题型:解答题
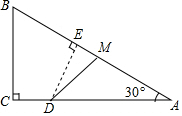 如图,Rt△ABC中,∠C=90°,∠A=30°,BC=6,点M在AB上,且AM=4,点D是AC边上的一个动点(不与A、C重合),设CD的长为x,△ADM的面积y
如图,Rt△ABC中,∠C=90°,∠A=30°,BC=6,点M在AB上,且AM=4,点D是AC边上的一个动点(不与A、C重合),设CD的长为x,△ADM的面积y查看答案和解析>>
科目:初中数学 来源: 题型:解答题
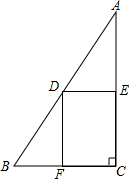 如图,在Rt△ABC中,∠C=90°,BC=6,AC=12,点D在斜边AB上,分别作DE⊥AC,DF⊥BC,垂足分别为点E,F,得四边形DECF,设DE=x,DF=y.
如图,在Rt△ABC中,∠C=90°,BC=6,AC=12,点D在斜边AB上,分别作DE⊥AC,DF⊥BC,垂足分别为点E,F,得四边形DECF,设DE=x,DF=y.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
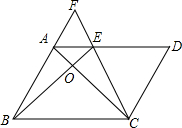 如图,点E是平行四边形ABCD边AD上一点,且AE=$\frac{1}{2}$ED,BA、CE的延长线交于点F,BE与AC交于点O,则下列结论:①相似三角形有2对,②AB=2AF,③8S△AOE=S△CED,④S四边形ABCE=2S△CED中正确的有( )
如图,点E是平行四边形ABCD边AD上一点,且AE=$\frac{1}{2}$ED,BA、CE的延长线交于点F,BE与AC交于点O,则下列结论:①相似三角形有2对,②AB=2AF,③8S△AOE=S△CED,④S四边形ABCE=2S△CED中正确的有( )| A. | 3个 | B. | 2个 | C. | 4个 | D. | 1个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com