
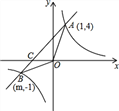
【题目】已知,如图,反比例函数y=![]() 的图象与一次函数y=x+b的图象交于点A(1,4),点B(m,-1),
的图象与一次函数y=x+b的图象交于点A(1,4),点B(m,-1),
(1)求一次函数和反比例函数的解析式;
(2)求△OAB的面积;
(3)直接写出不等式x+b>![]() 的解.
的解.
【答案】(1)y=![]() ,y=x+3;(2)
,y=x+3;(2)![]() ;(3)x>1或-4<x<0
;(3)x>1或-4<x<0
【解析】试题分析:(1)根据反比例函数y=![]() 的图象过点A(1,4)利用待定系数法求出即可;把B(m,﹣1)代入所求的反比例函数的解析式得出B点坐标,进而利用待定系数法求出一次函数解析式即可;
的图象过点A(1,4)利用待定系数法求出即可;把B(m,﹣1)代入所求的反比例函数的解析式得出B点坐标,进而利用待定系数法求出一次函数解析式即可;
(2)将三角形AOB分割为S△AOB=S△BOC+S△AOC,求出即可.
(3)根据函数的图象和交点坐标即可求得.
试题解析:解:(1)把A点坐标(1,4)分别代入y=![]() ,y=x+b,得:k=1×4,1+b=4,解得:k=4,b=3,∴反比例函数、一次函数的解析式分别为y=
,y=x+b,得:k=1×4,1+b=4,解得:k=4,b=3,∴反比例函数、一次函数的解析式分别为y=![]() ,y=x+3.
,y=x+3.
(2)当y=﹣1时,x=﹣4,∴B(﹣4,﹣1).又∵当y=0时,x+3=0,x=﹣3,∴C(﹣3,0),∴S△AOB=S△AOC+S△BOC=![]() ×4+
×4+![]() ×3×1=
×3×1=![]() .
.
(3)不等式x+b>![]() 的解是x>1或﹣4<x<0.
的解是x>1或﹣4<x<0.


科目:初中数学 来源: 题型:
【题目】某调查机构将今年温州市民最关注的热点话题分为消费、教育、环保、反腐及其它共五类.根据最近一次随机调查的相关数据,绘制的统计图表如下:
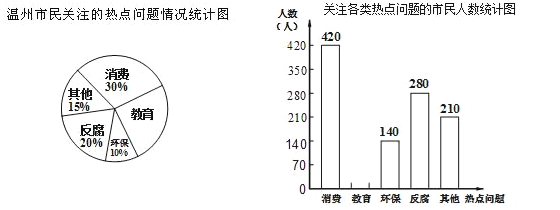
根据以上信息解答下列问题:
(1)本次共调查 人,请在答题卡上补全条形统计图并标出相应数据;
(2)若温州市约有900万人口,请你估计最关注教育问题的人数约为多少万人?
(3)在这次调查中,某单位共有甲、乙、丙、丁四人最关注教育问题,现准备从这四人中随机抽取两人进行座谈,求抽取的两人恰好是甲和乙的概率(列数状图或列表说明).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一些半径相同的小圆按如图所示的规律摆放,第1个图形有4个小圆,第2个图形有8个小圆,第3个图形有14个小圆,…,依次规律,第6个图形的小圆个数是( )

A. 56 B. 54 C. 44 D. 42
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】目前节能灯在城市已基本普及,今年云南省面向县级及农村地区推广,为相应号召,某商场计划用3800元购进节能灯120只,这两种节能灯的进价、售价如下表:

(1)求甲、乙两种节能灯各进多少只?
(2)全部售完120只节能灯后,该商场获利润多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
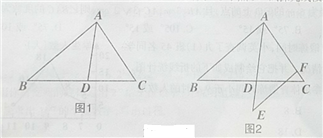
【题目】已知,如图1,AD是△ABC的角平分线,且AD=BD,
(1)求证:△CDA∽△CAB;
(2)若AD=6,CD=5,求AC的值;
(3)如图2,延长AD至E,使AE=AB,过E点作EF∥AB,交AC于点F,试探究线段EF
与线段AD的大小关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】网瘾低龄化问题已经引起社会各界的高度关注,有关部门在全国范围内对12﹣35岁的网瘾人群进行了简单的随机抽样调查,绘制出以下两幅统计图.
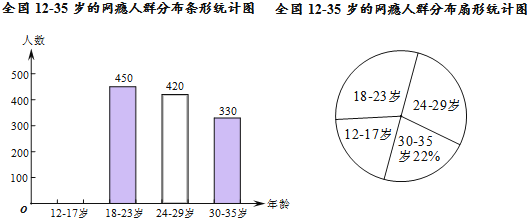
请根据图中的信息,回答下列问题:
(1)这次抽样调查中共调查了 人,并请补全条形统计图;
(2)扇形统计图中18﹣23岁部分的圆心角的度数是 度;
(3)据报道,目前我国12﹣35岁“网瘾人数”约为2000万,请估计其中12﹣17岁的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】垫球是排球队常规训练的重要项目之一.下列图表中的数据是甲、乙、丙三人每人十次垫球测试的成绩.测试规则为连续接球10个,每垫球到位1个记1分.
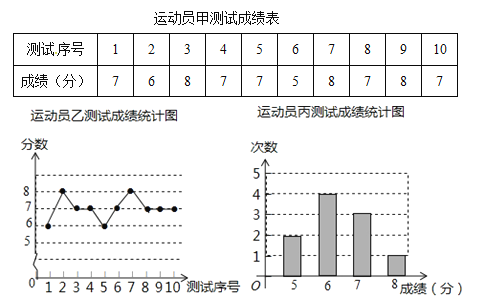
(1)写出运动员甲测试成绩的众数为_________;运动员乙测试成绩的中位数为_________;运动员丙测试成绩的平均数为_________;
(2)经计算三人成绩的方差分别为S甲2=0.8、S乙2=0.4、S丙2=0.8,请综合分析,在他们三人中选择一位垫球成绩优秀且较为稳定的接球能手作为自由人,你认为选谁更合适?为什么?
(3)甲、乙、丙三人相互之间进行垫球练习,每个人的球都等可能的传给其他两人,球最先从甲手中传出,第三轮结束时球回到甲手中的概率是多少?(用树状图或列表法解答)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形网格中每个小正方形边长都是1,小正方形的顶点称为格点,在正方形网格中分别画出下列图形:
![]() 在网格中画出长为
在网格中画出长为![]() 的线段AB.
的线段AB.
![]() 在网格中画出一个腰长为
在网格中画出一个腰长为![]() 、面积为3的等腰
、面积为3的等腰![]() DEF.
DEF.
(3)利用网格,可求出三边长分别为![]() ,
,![]() ,
,![]() 的三角形面积为__________
的三角形面积为__________
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com