


 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:初中数学 来源: 题型:
| 60 |
| 13 |
| A、4个 | B、3个 | C、2个 | D、1个 |
查看答案和解析>>
科目:初中数学 来源: 题型:
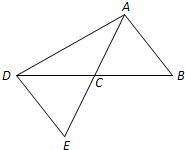 23、如图,A、B两点分别位于一池塘两侧,池塘左边有一水房D,在DB中点C处有一棵百年古槐,小明从A点出发,沿AC一直向前走到点E(A、C、E三点在同一条直线上),并使CE=CA,然后他测量出点E到水房D的距离,则DE的长度就是A、B两点间的距离.
23、如图,A、B两点分别位于一池塘两侧,池塘左边有一水房D,在DB中点C处有一棵百年古槐,小明从A点出发,沿AC一直向前走到点E(A、C、E三点在同一条直线上),并使CE=CA,然后他测量出点E到水房D的距离,则DE的长度就是A、B两点间的距离.查看答案和解析>>
科目:初中数学 来源: 题型:
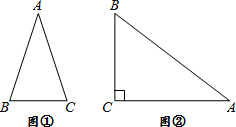 通过学习三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.类似的,可以在等腰三角形中建立边角之间的联系.我们定义:等腰三角形中底边与腰的比叫做顶角正对(sad),如图①,在△ABC中,AB=AC,顶角A的正对记作sadA,这时sadA=底边/腰=
通过学习三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.类似的,可以在等腰三角形中建立边角之间的联系.我们定义:等腰三角形中底边与腰的比叫做顶角正对(sad),如图①,在△ABC中,AB=AC,顶角A的正对记作sadA,这时sadA=底边/腰=| BC |
| AB |
| 3 |
| 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:
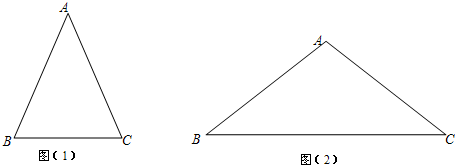
| 底边 |
| 腰 |
| BC |
| AB |
| 3 |
| 3 |
| 8 |
| 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com