下列说法正确的是( )A．“任意一个三角形的外角和等于180° 这一事件是不可能事件B．必然事件发生的概率为0C．一组数据1.6.3.9.8的极差为7D．“面积相等的两个三角形全等这一事件是必然事件题目和参考答案——青夏教育精英家教网—

3．下列说法正确的是（　　）

	A．	“任意一个三角形的外角和等于180°”这一事件是不可能事件
	B．	必然事件发生的概率为0
	C．	一组数据1，6，3，9，8的极差为7
	D．	“面积相等的两个三角形全等”这一事件是必然事件

分析利用事件的定义，以及概率的意义判断即可．

解答解：A、“任意一个三角形的外角和等于180°”这一事件是不可能事件，符合题意；
B、必然事件发生的概率为1，不符合题意；
C、一组数据1，6，3，9，8的极差为9-1=8，不符合题意；
D、“面积相等的两个三角形全等”这一事件是不确定事件，不符合题意，
故选A

点评此题考查了概率的意义，极差，以及随机事件，熟练掌握各自的性质是解本题的关键．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：解答题

13．已知一次函数y=（1-m）x-1+2m（m是常数）
（1）若该一次函数的图象经过原点，求m的值．
（2）若该一次函数的图象经过第一、二、三象限，求m的取值范囤．

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

14．

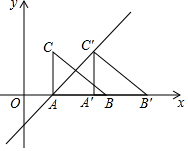如图，平面直角坐标系中，△ABC的两个顶点A、B的坐标分别为（2，0），（6，0），AC⊥x轴，BC=5，将△ABC沿x轴向右平移，得到△A′B′C′（A和A′，B和B′，C和C′分别是对应顶点），直线y=x+b经过点A，C′，则点C′的坐标为（　　）

A．

（5，3）

B．

（3，5）

C．

（6，4）

D．

（4，6）

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

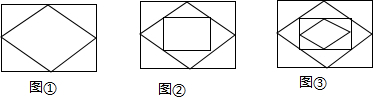
11．已知：顺次连接矩形各边的中点，得到一个菱形，如图①；再顺次连接菱形各边的中点，得到一个新的矩形，如图②；然后顺次连接新的矩形各边的中点，得到一个新的菱形，如图③；如此反复操作下去，则第2017个图形中直角三角形的个数有（　　）

A．

8072个

B．

4036个

C．

4032个

D．

2016个

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

18．

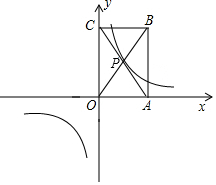阅读理解：实数a＞0，b＞0，∵（$\sqrt{a}$-$\sqrt{b}}$）²≥0，∴a-2$\sqrt{ab}$+b≥0，即a+b≥2$\sqrt{ab}$．若ab=m（m为定值），则a+b≥2$\sqrt{m}$，当且仅当a=b时等式成立，即a=b时，a+b=2$\sqrt{m}$，∴当a=b=$\sqrt{m}$时，a+b取得最小值（填“最大”或“最小”）．
理解应用：函数y=x+$\frac{2}{x}$（x＞0），当x=$\sqrt{2}$时，y_最小值=2$\sqrt{2}$．
拓展应用：如图，双曲线y=$\frac{4}{x}$经过矩形OABC的对角线交点P，求矩形OABC的最小周长．

查看答案和解析>>

科目：初中数学 来源： 题型：填空题

8．关于x的一元二次方程kx²-3x-1=0有实数根，则k的取值范围是k≥-$\frac{9}{4}$且k≠0．

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

15．