
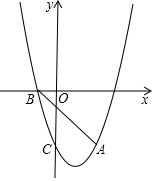
 如图,抛物线y=ax2+bx-3经过点A(2,-3),与x轴负半轴交于点B,与y轴交于点C,且OC=3OB.
如图,抛物线y=ax2+bx-3经过点A(2,-3),与x轴负半轴交于点B,与y轴交于点C,且OC=3OB.分析 (1)待定系数法即可得到结论;
(2)连接AC,作BF⊥AC交AC的延长线于F,根据已知条件得到AF∥x轴,得到F(-1,-3),设D(0,m),则OD=|m|即可得到结论;
(3)设M(a,a2-2a-3),N(1,n),①以AB为边,则AB∥MN,AB=MN,如图2,过M作ME⊥对称轴y于E,AF⊥x轴于F,于是得到△ABF≌△NME,证得NE=AF=3,ME=BF=3,得到M(4,5)或(-2,11);②以AB为对角线,BN=AM,BN∥AM,如图3,则N在x轴上,M与C重合,于是得到结论.
解答 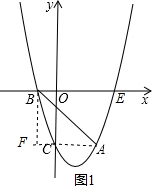 解:(1)由y=ax2+bx-3得C(0.-3),
解:(1)由y=ax2+bx-3得C(0.-3),
∴OC=3,
∵OC=3OB,
∴OB=1,
∴B(-1,0),
把A(2,-3),B(-1,0)代入y=ax2+bx-3得$\left\{\begin{array}{l}{4a+2b-3=-3}\\{a-b-3=0}\end{array}\right.$,
∴$\left\{\begin{array}{l}{a=1}\\{b=-2}\end{array}\right.$,
∴抛物线的解析式为y=x2-2x-3;
(2)设连接AC,作BF⊥AC交AC的延长线于F,
∵A(2,-3),C(0,-3),
∴AF∥x轴,
∴F(-1,-3),
∴BF=3,AF=3,
∴∠BAC=45°,
设D(0,m),则OD=|m|,
∵∠BDO=∠BAC,
∴∠BDO=45°,
∴OD=OB=1,
∴|m|=1,
∴m=±1,
∴D1(0,1),D2(0,-1);
(3)设M(a,a2-2a-3),N(1,n),
①以AB为边,则AB∥MN,AB=MN,如图2,过M作ME⊥对称轴y于E,AF⊥x轴于F,
则△ABF≌△NME,
∴NE=AF=3,ME=BF=3,
∴|a-1|=3,
∴a=4或a=-2,
∴M(4,5)或(-2,5);
②以AB为对角线,BN=AM,BN∥AM,如图3,
则N在x轴上,M与C重合,
∴M(0,-3),
综上所述,存在以点A,B,M,N为顶点的四边形是平行四边形,M(4,5)或(-2,5)或(0,-3).
点评 本题考查了待定系数法求二次函数的解析式,全等三角形的判定和性质,平行四边形的判定和性质,正确的作出图形是解题的关键.


科目:初中数学 来源: 题型:解答题
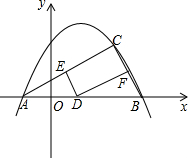 如图,已知抛物线y=-$\frac{1}{2}{x^2}$+bx+c图象经过A(-1,0),B(4,0)两点.
如图,已知抛物线y=-$\frac{1}{2}{x^2}$+bx+c图象经过A(-1,0),B(4,0)两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
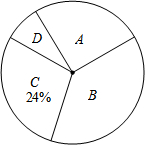 近期电视剧《人民的名义》热播,某校“话剧表演”社团在本校学生中开展学生知晓情况专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为A、B、C、D四类.其中,A类表示“自己看过”,B类表示“听家长讲过”,
近期电视剧《人民的名义》热播,某校“话剧表演”社团在本校学生中开展学生知晓情况专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为A、B、C、D四类.其中,A类表示“自己看过”,B类表示“听家长讲过”,| 类别 | A | B | C | D |
| 频数 | 30 | 40 | 24 | b |
| 频率 | a | 0.4 | 0.24 | 0.06 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
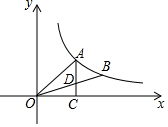 如图,A、B是双曲线y=$\frac{k}{x}$上的两点,过A点作AC⊥x轴,交OB于D点,垂足为C.若D为OB的中点,△ADO的面积为3,则k的值为8.
如图,A、B是双曲线y=$\frac{k}{x}$上的两点,过A点作AC⊥x轴,交OB于D点,垂足为C.若D为OB的中点,△ADO的面积为3,则k的值为8.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,点O(0,0),A(0,1)是正方形OAA1B的两个顶点,以对角线OA1为边作正方形OA1A2B1,再以对角线OA2为边作正方形OA2A3B2,…,依此规律,点A2017的坐标是(21008,21008).
如图,点O(0,0),A(0,1)是正方形OAA1B的两个顶点,以对角线OA1为边作正方形OA1A2B1,再以对角线OA2为边作正方形OA2A3B2,…,依此规律,点A2017的坐标是(21008,21008).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
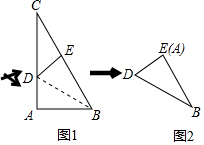 在三角形纸片ABC中,∠A=90°,∠C=30°,AC=30cm,将该纸片沿过点B的直线折叠,使点A落在斜边BC上的一点E处,折痕记为BD(如图1),减去△CDE后得到双层△BDE(如图2),再沿着过△BDE某顶点的直线将双层三角形剪开,使得展开后的平面图形中有一个是平行四边形,则所得平行四边形的周长为40或$\frac{80\sqrt{3}}{3}$cm.
在三角形纸片ABC中,∠A=90°,∠C=30°,AC=30cm,将该纸片沿过点B的直线折叠,使点A落在斜边BC上的一点E处,折痕记为BD(如图1),减去△CDE后得到双层△BDE(如图2),再沿着过△BDE某顶点的直线将双层三角形剪开,使得展开后的平面图形中有一个是平行四边形,则所得平行四边形的周长为40或$\frac{80\sqrt{3}}{3}$cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
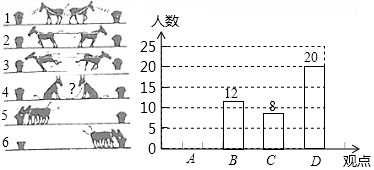 主题班会课上,王老师出示了如图所示的一幅漫画,经过同学们的一番热议,达成以下四个观点:
主题班会课上,王老师出示了如图所示的一幅漫画,经过同学们的一番热议,达成以下四个观点:| 观点 | 频数 | 频率 |
| A | a | 0.2 |
| B | 12 | 0.24 |
| C | 8 | b |
| D | 20 | 0.4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com