
分析 解绝对值不等式的方法是想办法去掉绝对值符号,转化成已学过的不等式(组)来解决.
解答 解:①当x≥2时,原不等式变形为:$\left\{\begin{array}{l}{x≥2}\\{x-2+x+1>5}\end{array}\right.$,解不等式组得到:x>3.
②当x<-1时,原不等式变形为:$\left\{\begin{array}{l}{x<-1}\\{2-x-x-x>5}\end{array}\right.$; 解不等式组得:x<-3.
③当-1≤x<2时,元不等式变形为:$\left\{\begin{array}{l}{-1≤x<2}\\{2-x+x+1<5}\end{array}\right.$,无解.
综合①②③可得,原不等式的解集为x>3或x<-3.
点评 本题主要考查分式不等式的解法,体现了等价转化和分类讨论的数学思想,属于基础题.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
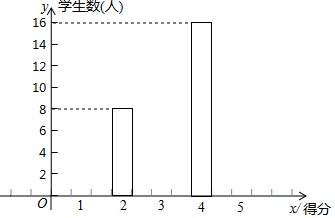
| 得分 | 人数 | 频率 |
| 1 | m | 0.1 |
| 2 | 8 | p |
| 3 | n | 0.2 |
| 4 | 16 | 0.4 |
| 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
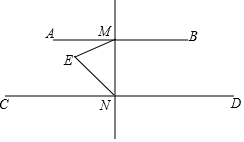 如图,AB∥CD,MN⊥AB于M.
如图,AB∥CD,MN⊥AB于M.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com