
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是边
是边![]() 上的一个动点,将
上的一个动点,将![]() 沿
沿![]() 折叠,得到
折叠,得到![]() .连接
.连接![]() 、
、![]() ,若
,若![]() 为等腰三角形,则
为等腰三角形,则![]() 的长为_______.
的长为_______.

【答案】![]() 、
、![]() 、
、![]()
【解析】
当的B′在矩形的内部时,分三种情形考虑:①DA=DB′.②AD=AB′.③B′A=B′D.当点B′落在矩形的外部时,有一种情形DA=DB′,分别求解即可.
解:如图,过点B′作MN⊥CD于M,交AB于N,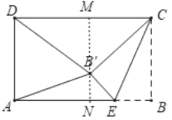
∵四边形ABCD是矩形,
∴AD=BC=13,CD=AB=24,∠ABC=∠BCD=∠CDA=∠DAB=90°,
又∵MN⊥CD,
∴四边形ANMD是矩形,四边形BCMN是矩形,
∴AD=MN=13,AN=DM,MC=BN,
若AD=DB′=13,
∵将△CBE沿CE折叠,得到△CB′E连接AB′,
∴BC=B′C=13,BE=B′E,
∴B′C=B′D,
又∵MN⊥CD,
∴CM=DM=12,
∴B′M=![]() ,
,
∴B′N=13-5=8,
∵B′E2=NE2+B′N2,
∴BE2=64+(12BE)2,
∴BE=![]() ;
;
∵AB′的最小值=ACCB′=![]() ,
,
AB′>AD,
当B′A=B′D时,
∵B′M=B′N,
∴CB′=2B′M,
∴∠B′CM=30°,
∴∠ECB=∠ECB′=30°,
∴BE=CBtan30°=![]() ,
,
如图当点B′在直线CD的上方,AD=DB′时,
同法可知DM=CM=12,MB′=5,
在Rt△ENB′中,则有BE2=(BE12)2+182,
解得BE=![]() ,
,
综上所述,满足条件的BE的值为![]() 或
或![]() 或
或![]() ,
,
故答案为:![]() 、
、![]() 、
、![]()


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】学校团委发起“爱心储蓄”活动,鼓励学生将自己的压岁钱存入银行,定期一年,到期后取回本金,而把利息捐给家庭贫困的儿童.学校共有学生1200人全部参加了此项活动,图1是该校各年级学生人数比例分布的扇形统计图,图2是该校学生人均存款情况的条形统计图.
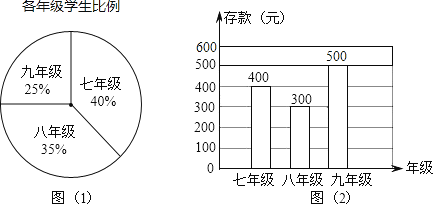
(1)求该学校的人均存款数;
(2)若银行一年定期存款的年利率是2.25%,且每702元能提供给1位家庭贫困儿童一年的基本费用,那么该学校一年能够帮助多少位家庭贫困儿童?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,4),B(4,2),C(3,5)(每个方格的边长均为1个单位长度).
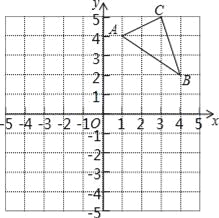
(1)请画出△A1B1C1,使△A1B1C1与△ABC关于x轴对称;
(2)将△ABC绕点O逆时针旋转90°,画出旋转后得到的△A2B2C2,并直接写出点B旋转到点B2所经过的路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
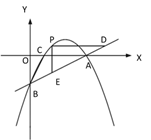
【题目】【题目】如图①,一次函数 y=![]() x - 2 的图像交 x 轴于点 A,交 y 轴于点 B,二次函数 y=
x - 2 的图像交 x 轴于点 A,交 y 轴于点 B,二次函数 y=![]() x2 bx c的图像经过 A、B 两点,与 x 轴交于另一点 C.
x2 bx c的图像经过 A、B 两点,与 x 轴交于另一点 C.
(1)求二次函数的关系式及点 C 的坐标;
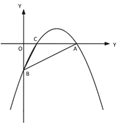
(2)如图②,若点 P 是直线 AB 上方的抛物线上一点,过点 P 作 PD∥x 轴交 AB 于点 D,PE∥y 轴交 AB 于点 E,求 PD+PE 的最大值;
(3)如图③,若点 M 在抛物线的对称轴上,且∠AMB=∠ACB,求出所有满足条件的点 M的坐标.
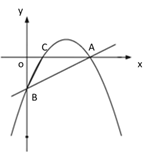
① ② ③
查看答案和解析>>
科目:初中数学 来源: 题型:
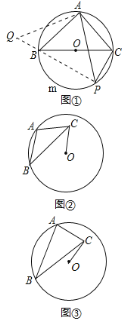
【题目】(1)问题背景:如图①,BC是⊙O的直径,点A在⊙O上,AB=AC,P为![]() 上一动点(不与B,C重合),求证:
上一动点(不与B,C重合),求证:![]() PA=PB+PC.请你根据图中所给的轴助线,给出作法并完成证明过程.
PA=PB+PC.请你根据图中所给的轴助线,给出作法并完成证明过程.
(2)类比迁移:如图②,⊙O的半径为3,点A,B在⊙O上,C为⊙O内一点,AB=AC,AB⊥AC,垂足为A,求OC的最小值
(3)拓展延伸:如图③,⊙O的半径为3,点A,B在⊙O上,C为⊙O内一点,AB=![]() AC,AB⊥AC,垂足为A,则OC的最小值为____________.
AC,AB⊥AC,垂足为A,则OC的最小值为____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,AB=4,BC=2,正方形ADEF的边长为2,F、A、B在同一直线上,正方形ADEF向右平移到点F与B重合,点F的平移距离为x,平移过程中两图重叠部分的面积为y,则y与x的关系的函数图象表示正确的是( )
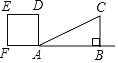
A.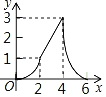 B.
B.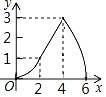
C.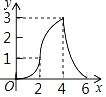 D.
D.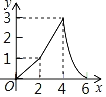
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,开口向下的抛物线与![]() 轴交于点
轴交于点![]() 、
、![]() ,与
,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 是第一象限内抛物线上的一点.
是第一象限内抛物线上的一点.
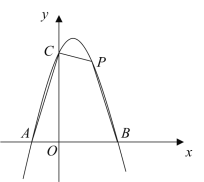
(1)求该抛物线所对应的函数解析式;
(2)设四边形![]() 的面积为
的面积为![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com