
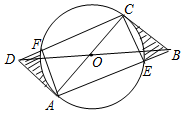
 已知:如图,AC是⊙O的直径,圆心为点O,过A,C两点分别作⊙的切线,过圆心O的直线分别交这两条切线于B,D.
已知:如图,AC是⊙O的直径,圆心为点O,过A,C两点分别作⊙的切线,过圆心O的直线分别交这两条切线于B,D.分析 (1)首先利用全等三角形的判定定理得△AOD≌△COB,由全等三角形的性质可得OB=OD,又OA=OC,由平行四边形的判定定理可得结论;
(2)利用平行线的性质可得CF∥AE;由平行线的性质可得∠ACF=∠CAE,由圆周角定理易得∠AFC=∠CEA=90°,易得△ACF≌△CEA;由全等三角形的性质可得AE=CF,易得结论;
(3)首先求得∠BAC和∠COE的度数,利用扇形的面积公式求得扇形OEC的面积,阴影部分的面积为2倍的三角形ABC的面积减去扇形OCE的面积再减去三角形AOE的面积.
解答 解:(1)证明:
∵AC为⊙O的直径,
∴OA=OC;
∵BC,AD分别是⊙O的切线,
∴∠OCB=∠OAD=90°;
∵∠AOD=∠COB,
在△AOD与△COB中,
$\left\{\begin{array}{l}{∠OCB=∠OAD}\\{OC=OA}\\{∠COB=∠AOD}\end{array}\right.$,
∴△AOD≌△COB;
∴OB=OD;
∴四边形ABCD是平行四边形.
(2)∵四边形ABCD是平行四边形.
∴CF∥AE;
∴∠ACF=∠CAE;
∵AC为⊙O的直径,
∴∠AFC=∠CEA=90°;
在△ACF与△CEA中,
$\left\{\begin{array}{l}{∠ACF=∠CAE}\\{∠AFC=CEA}\\{AC=CA}\end{array}\right.$,
∴△ACF≌△CEA;
∴AE=CF;
∴四边形AECF是平行四边形;
∴四边形AECF是矩形.
(3)连接EO,
∵⊙O的半径为3,
∴AC=6,
∵BC=$2\sqrt{3}$,
在Rt△ABC中,tan∠BAC=$\frac{2\sqrt{3}}{6}$=$\frac{\sqrt{3}}{3}$,
∴∠BAC=30°;
∴∠COE=60°;
所以扇形OEC的面积=$\frac{60}{360}π×{3}^{2}$=$\frac{3}{2}π$
所以S阴影=2(S△ABC-$\frac{3}{2}π$-S△AOE)=2($\frac{1}{2}×6×2\sqrt{3}-\frac{3}{2}π$-$\frac{1}{2}×3×3×sin120°$)=$\frac{15}{2}$$\sqrt{3}$-3π.
点评 本题主要考查了切线的性质,矩形和平行四边形的判定定理,熟练掌握矩形和平行四边形的判定定理是解答此题的关键.


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:初中数学 来源: 题型:解答题
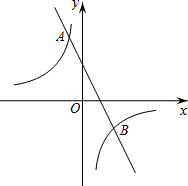 如图,在平面直角坐标系xOy中,双曲线y=$\frac{m}{x}$与直线y=-2x+1交于点A(-1,a)
如图,在平面直角坐标系xOy中,双曲线y=$\frac{m}{x}$与直线y=-2x+1交于点A(-1,a)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
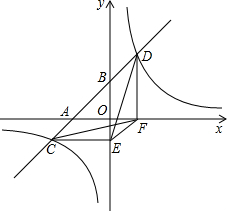 如图,一次函数y=ax+b的图象与x轴,y轴交于A,B两点,与反比例函数$y=\frac{k}{x}$的图象相交于C,D两点,分别过C,D两点作y轴,x轴的垂线,垂足为E,F,连接CF,DE.有下列四个结论:
如图,一次函数y=ax+b的图象与x轴,y轴交于A,B两点,与反比例函数$y=\frac{k}{x}$的图象相交于C,D两点,分别过C,D两点作y轴,x轴的垂线,垂足为E,F,连接CF,DE.有下列四个结论:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
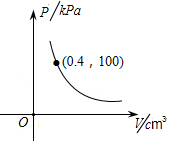 某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P(Kpa)是气体体积V(cm3)的反比例函数,其图象如图所示,当气球内气压大于120Kpa时,气球将爆炸,为了安全,该气球内气体体积V(cm3)的取值范围是V≥$\frac{1}{3}$.
某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P(Kpa)是气体体积V(cm3)的反比例函数,其图象如图所示,当气球内气压大于120Kpa时,气球将爆炸,为了安全,该气球内气体体积V(cm3)的取值范围是V≥$\frac{1}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com