
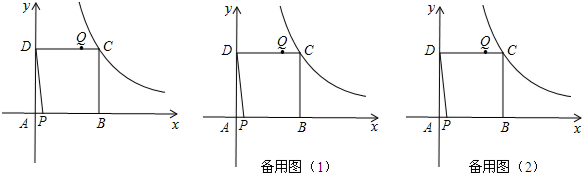
���� ��1�����ô���ϵ�������ɽ�����⣻
��2����DQ=PB���г����̼��ɽ�����⣻
��3���������������ۢٵ�0��t��1ʱ��S=$\frac{1}{2}$DQ•CB���ڵ�1��t��2ʱ��S=$\frac{1}{2}$•BQ•AD���۵�2��t��$\frac{12}{5}$ʱ��S=$\frac{1}{2}$•BQ•AD��
��� �⣺��1���跴���������Ľ���ʽΪy=$\frac{k}{x}$��
�߷���������������C��4��4����
��k=16��
�෴���������Ľ���ʽΪy=$\frac{16}{x}$��
�ʴ�Ϊy=$\frac{16}{x}$��
��2��������AP=t��DQ=4t��
���ı���PBQD��ƽ���ı��Σ�
��DQ=PB��
��4t=4-t��
��t=$\frac{4}{5}$��
�൱t=$\frac{4}{5}$ʱ���ı���PBQD��ƽ���ı��Σ�
��3������P���Q����ʱ��t+4t=12��t=$\frac{12}{5}$��
�ٵ�0��t��1ʱ��
S=$\frac{1}{2}$DQ•CB=$\frac{1}{2}$•4t•4=8t��
�ڵ�1��t��2ʱ��
S=$\frac{1}{2}$•BQ•AD=$\frac{1}{2}$•��8-4t��•4=16-8t��
�۵�2��t��$\frac{12}{5}$ʱ��
S=$\frac{1}{2}$•BQ•AD=$\frac{1}{2}$•��4t-8��•4=8t-16��
��S=$\left\{\begin{array}{l}{8t}&{��0��t��1��}\\{16-8t}&{��1��t��2��}\\{8t-16}&{��2��t��\frac{12}{5}��}\end{array}\right.$��
��t=1ʱ����BDQ��������
���� ���⿼�鷴���������ۺ��⡢�����ε����ʡ�ƽ���ı��ε��ж��������ε������֪ʶ������Ĺؼ������������ѧ֪ʶ������⣬ѧ���÷������۵�˼��˼�����⣬�����п�ѹ���⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
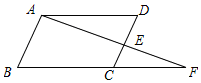 ��ͼ����C��E�ֱ����߶�BF���߶�CD���е㣬AD��BF��
��ͼ����C��E�ֱ����߶�BF���߶�CD���е㣬AD��BF���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
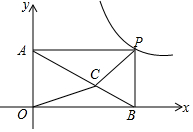 ��ͼ��P��˫����y=$\frac{6}{x}$��x��0��������һ�㣬��PB��x����B��PA��y����A��C��ƽ���ı���OAPB������һ�㣬����CA��CO��CB��CP�����OCB���ACP������͵��ڣ�������
��ͼ��P��˫����y=$\frac{6}{x}$��x��0��������һ�㣬��PB��x����B��PA��y����A��C��ƽ���ı���OAPB������һ�㣬����CA��CO��CB��CP�����OCB���ACP������͵��ڣ�������| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -$\frac{1}{4}$ | B�� | -4 | C�� | 4 | D�� | $\frac{1}{4}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
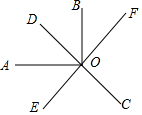 ��ͼ����ֱ֪��CD��EF�ཻ�ڵ�O��OA��OB����OEƽ�֡�AOC������EOC=60�㣬���BOF=30�㣮
��ͼ����ֱ֪��CD��EF�ཻ�ڵ�O��OA��OB����OEƽ�֡�AOC������EOC=60�㣬���BOF=30�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com