解:(1)设发放树苗点离A处x(0≤x≤700)米,所有学生到发放树苗点的距离的和为y米,
则:①当0≤x≤300时,有y=20x+40(300-x)+30(700-x)=-50x+33000,
②当300<x≤700时,有y=20x+40(x-300)+30(700-x)=30x+9000,
①中x=300时,y有最小值18000,
②中y>18000,
∴按方案①设点,发放树苗点应设在距离A处300米处,即B处.
(2)设发放树苗点距离A处x(0≤x≤700)米,
则:①当0≤x≤300时,有:20x+30(700-x)=40(300-x),
解得x=-300(不合题意,舍去),
②当300<x≤700时,有:20x+30(700-x)=40(x-300),
解得:x=660,
∴按方案二设点,发放树苗点应设在距离A处660米.
(3)设甲小组减小a(a<20)人,
由(2)得:(20-a)x+30(700-x)=40(x-300)(300<x≤700),
解得:

,
又∵
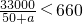
,且a越大,x越小
∴若甲小组减少人数则发放树苗点离B处越来越近.
分析:(1)设发放树苗点离A处x(0≤x≤700)米,所有学生到发放树苗点的距离的和为y米,然后将x进行分段处理,分别得出最小值,从而可得出答案.
(2)设发放树苗点距离A处x(0≤x≤700)米,根据甲组与丙组的所有学生到发放树苗点距离的和等于乙组所有学生到发放树苗点距离的和可列出方程,解出符合条件的解即可.
(3)设甲小组减小a(a<20)人,根据(2)的条件可列出方程,解出x的表达式即可作出说明.
点评:本题考查一次函数的应用,有一定的难度,解答此类题目的方法是根据题意所述的等价关系列出函数解析式,然后分段处理函数,得出符合题意的结果.

 ,
,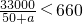 ,且a越大,x越小
,且a越大,x越小

 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案