
【题目】如图,AB是⊙O的直径,AC是⊙O的切线,切点为A,BC交⊙O于点D,点E是AC的中点.
(1)试判断直线DE与⊙O的位置关系,并说明理由;
(2)若⊙O的半径为2,∠B=50°,AC=4.8,求图中阴影部分的面积.
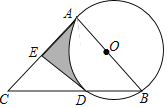
【答案】(1)直线DE与⊙O相切.理由见解析;(2)图中阴影部分的面积为4.8﹣![]() π.
π.
【解析】(1)连接OE、OD,如图,根据切线的性质得∠OAC=90°,再证明△AOE≌△DOE得到∠ODE=∠OAE=90°,然后根据切线的判定定理得到DE为⊙O的切线;
(2)先计算出∠AOD=2∠B=100°,利用四边形的面积减去扇形的面积计算图中阴影部分的面积.
(1)直线DE与⊙O相切.理由如下:
连接OE、OD,如图,
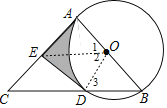
∵AC是⊙O的切线,
∴AB⊥AC,
∴∠OAC=90°,
∵点E是AC的中点,O点为AB的中点,
∴OE∥BC,
∴∠1=∠B,∠2=∠3,
∵OB=OD,
∴∠B=∠3,
∴∠1=∠2,
在△AOE和△DOE中
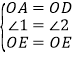 ,
,
∴△AOE≌△DOE,
∴∠ODE=∠OAE=90°,
∴OA⊥AE,
∴DE为⊙O的切线;
(2)∵点E是AC的中点,
∴AE=![]() AC=2.4,
AC=2.4,
∵∠AOD=2∠B=2×50°=100°,
∴图中阴影部分的面积=2×![]() ×2×2.4﹣
×2×2.4﹣![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,菱形OABC的顶点O是原点,顶点B在y轴上,两条对角线AC、OB的长分别是6和4,反比例函数![]() 的图象经过点C.
的图象经过点C.
(1)写出点A的坐标,并求k的值;
(2)将菱形OABC沿y轴向下平移多少个单位长度后点A会落在该反比例函数的图象上?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把△ABC先向上平移3个单位长度,再向右平移2个单位长度,得到△A1B1C1.

(1)在图中画出△A1B1C1,并写出点A1、B1、C1的坐标;
(2)连接A1A、C1C,则四边形A1ACC1的面积为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一只不透明袋子中装有三只大小、质地都相同的小球,球面上分别标有数字1、﹣2、3,搅匀后先从中任意摸出一个小球(不放回),记下数字作为点A的横坐标,再从余下的两个小球中任意摸出一个小球,记下数字作为点A的纵坐标.
(1)用画树状图或列表等方法列出所有可能出现的结果;
(2)求点A落在第四象限的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB,CD,EF相交于点O.
(1)写出∠COE的邻补角;
(2)分别写出∠COE和∠BOE的对顶角;
(3)如果∠BOD=60°,∠BOF=90°,求∠AOF和∠FOC的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OP平分∠AOB,PA⊥OA,PB⊥OB,垂足分别为A,B.下列结论中:①PA=PB;②△AOP≌△BOP;③OA=OB;④PO平分∠APB.其中成立的有________(填写正确的序号).

查看答案和解析>>
科目:初中数学 来源: 题型:
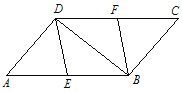
【题目】如图,在□ABCD 中,∠ADB=90°,点 E 为 AB 边的中点,点 F 为CD 边的中点.
(1)求证:四边形 DEBF 是菱形;
(2)当∠A 等于多少度时,四边形 DEBF 是正方形?并说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,C、D是垂足,连接CD,且交OE于点F.
(1)求证:OE是CD的垂直平分线.
(2)若∠AOB=60,请你探究OE,EF之间有什么数量关系?并证明你的结论。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com