
【题目】如图,抛物线的表达式为y=ax2+4ax+4a-1(a≠0),它的图像的顶点为A,与x轴负半轴相交于点B、点C(点B在点C左侧),与y轴交于点D,连接AO交抛物线于点E,且S△AEC:S△CEO=1:3.
(1)求点A的坐标和抛物线表达式;
(2)在抛物线的对称轴上是否存在一点P,使得△BDP的内心也在对称轴上,若存在,求点P的坐标;若不存在,请说明理由;
(3)连接BD,点Q是y轴左侧抛物线上的一点,若以Q为圆心,![]() 为半径的圆与直线BD相切,求点Q的坐标.
为半径的圆与直线BD相切,求点Q的坐标.
【答案】(1)抛物线表达式为y=x2+4x+3 ;(2)P(-2,-3);(3)Q(-4,3).
【解析】
(1)根据抛物线的对称轴易求得顶点坐标,再根据S△AEC:S△CEO=1:3,求得OE:OA=3:4,再证得△OFE∽△OMA,求得点E的坐标,从而求得答案;
(2)根据内心的定义知∠BPM=∠DPM,设点P(-2,b),根据三角函数的定义求得![]() ,继而求得
,继而求得![]() 的值,从而求得答案;
的值,从而求得答案;
(3)设Q(m,m2+4m+3),分类讨论,①点Q在BD左上方抛物线上,②点Q在BD下方抛物线上,利用![]() 的不同计算方法求得
的不同计算方法求得![]() 的值,从而求得答案.
的值,从而求得答案.
(1)由抛物线y=ax2+4ax+4a-1得对称轴为直线![]() ,当
,当![]() 时,
时,![]() ,
,
∴![]() ,
,
∵S△AEC:S△CEO=1:3 ,
∴AE:OE=1:3 ,
∴OE:OA=3:4,
过点E作EF⊥x轴,垂足为点F,设对称轴与x轴交点为M,如图,
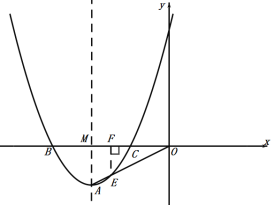
∵EF//AM ,
∴△OFE∽△OMA ,
∴ ![]() ,
,
∴![]() ,
,
∴![]() ,
,
把点![]() 代入抛物线表达式y=ax2+4ax+4a-1得
代入抛物线表达式y=ax2+4ax+4a-1得
![]() ,
,
解得:a=1,
∴抛物线表达式为:y=x2+4x+3 ;
(2)三角形的内心是三个角平分线的交点,
∴∠BPM=∠DPM,
过点D作DH⊥AM,垂足为点H,设点P(-2,b),
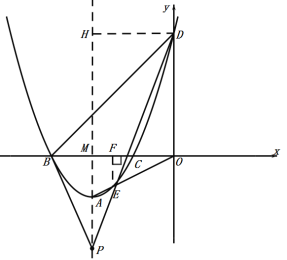
∵tan∠BPM=tan∠DPM ,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴P(-2,-3),
(3)∵抛物线表达式为:y=x2+4x+3 ,
∴抛物线与![]() 轴和
轴和![]() 轴的交点坐标分别为:B(-3,0) ,C(-1,0) ,D(0,3) ,
轴的交点坐标分别为:B(-3,0) ,C(-1,0) ,D(0,3) ,
∴![]() ,
,
∴![]()
设Q(m,m2+4m+3),
①点Q在BD左上方抛物线上,如图:作BG⊥x轴交BD于G,QF⊥x轴交于F,作QE⊥BD于E,
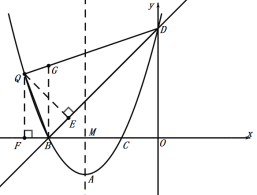
设直线QD的解析式为:![]() ,
,
∵点Q的坐标为(m,m2+4m+3)代入![]() 得:
得:![]() ,
,
∴直线QD的解析式为:![]() ,
,
当![]() 时,
时,![]() ,
,
∴点G的坐标为;![]() ,
,
∴![]()
![]() ,
,
∵![]() ,
,
∴![]() ,
,
即:![]() ,
,
解得:![]() 或
或![]() (不合题意,舍去) ,
(不合题意,舍去) ,
∴点![]() 的坐标为:
的坐标为:);
②点Q在BD下方抛物线上,如图:QF⊥x轴交于F,交BD于G,作QE⊥BD于E,
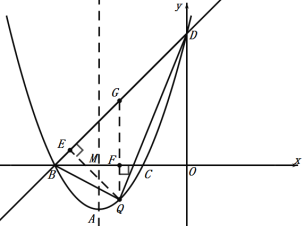
设直线BD的解析式为:![]() ,
,
将点B(-3,0)代入![]() 得:
得:![]() ,
,
∴直线BD的解析式为:![]() ,
,
当![]() 时,
时,![]() ,
,
∴点G的坐标为;![]() ,
,
∴![]()
![]() ,
,
∵![]() ,
,
∴![]() ,
,
即:![]() ,
,
∵![]()
∴方程无解,
综上:点![]() 的坐标为:
的坐标为:![]() ).
).


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源: 题型:
【题目】(发现)在解一元二次方程的时候,发现有一类形如x2+(m+n)x+mn=0的方程,其常数项是两个因数的积,而它的一次项系数恰好是这两个因数的和,则我们可以把它转化成x2+(m+n)x+mn=(m+x)(m+n)=0
(探索)解方程:x2+5x+6=0:x2+5x+6=x2+(2+3)x+2×3=(x+2)(x+3),原方程可转化为(x+2)(x+3)=0,即x+2=0或x+3=0,进而可求解.
(归纳)若x2+px+q=(x+m)(x+n),则p= q= ;
(应用)
(1)运用上述方法解方程x2+6x+8=0;
(2)结合上述材料,并根据“两数相乘,同号得正,异号得负“,求出一元二次不等式x2﹣2x﹣3>0的解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如图所示,则下列代数式:ab,ac,a+b+c,a-b+c, 2a+b,2a-b中,其值为正的代数式的个数为( )
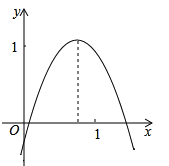
A.2个B.3个C.4个D.4个以上
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近几年购物的支付方式日益增多,某数学兴趣小组就此进行了抽样调查.调查结果显示,支付方式有:A微信、B支付宝、C现金、D其他,该小组对某超市一天内购买者的支付方式进行调查统计,得到如下两幅不完整的统计图.

请你根据统计图提供的信息,解答下列问题:
(1)本次一共调查了多少名购买者?
(2)请补全条形统计图;在扇形统计图中A种支付方式所对应的圆心角为 度.
(3)若该超市这一周内有1600名购买者,请你估计使用A和B两种支付方式的购买者共有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,要在木里县某林场东西方向的两地之间修一条公路MN,已知点C周围200 m范围内为原始森林保护区,在MN上的点A处测得C在A的北偏东45°方向上,从A向东走600 m到达B处,测得C在点B的北偏西60°方向上.
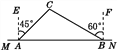
(1)MN是否穿过原始森林保护区?为什么?(参考数据: ![]() ≈1.732)
≈1.732)
(2)若修路工程顺利进行,要使修路工程比原计划提前5天完成,需将原定的工作效率提高25%,则原计划完成这项工程需要多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,Rt△ABC中,∠ACB=90°,点D为AB边上的动点(点D不与点A,点B重合),过点D作ED⊥CD交直线AC于点E,已知∠A=30°,AB=4cm,在点D由点A到点B运动的过程中,设AD=xcm,AE=ycm.
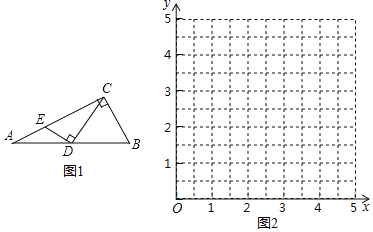
(1)通过取点、画图、测量,得到了x与y的几组值,如表:

小东根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.下面是小东的探究过程,请补充完整:(说明:补全表格时相关数值,保留一位小数)
(2)在如图2的平面直角坐标系xOy中,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;
(3)结合画出的函数图象,解决问题:当AE=![]() AD时,AD的长度约为 cm.
AD时,AD的长度约为 cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在由边长为1的小正方形组成的网格中,△ABC的顶点均落在格点上.
(1)将△ABC绕点O顺时针旋转90°后,得到△A1B1C1.在网格中画出△A1B1C1;
(2)求线段OA在旋转过程中扫过的图形面积;(结果保留π)
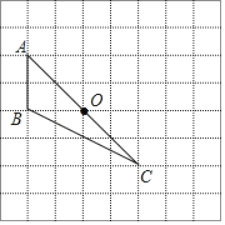
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在锐角三角形ABC中,点D,E分别在边AC,AB上,AG⊥BC于点G,AF⊥DE于点F,∠EAF=∠GAC.
(1)求证:△ADE∽△ABC;
(2)若AD=3,AB=5,求![]() 的值.
的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com