
如图8,对称轴为直线x=2的抛物线经过点A(-1,0),C(0,5)两点,与x轴另一交点为B,已知M(0,1),E(a,0),F(a+1,0),点P是第一象限内的抛物线上的动点.
(1)求此抛物线的解析式.
(2)当a=1时,求四边形MEFP面积的最大值,并求此时点P的坐标.
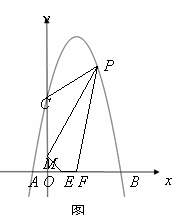 (3)若△PCM是以点P为顶点的等腰三角形,求a为何值时,四边形PMEF周长最小?请说明理由.
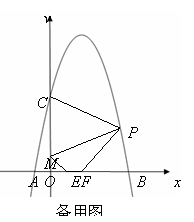
(3)若△PCM是以点P为顶点的等腰三角形,求a为何值时,四边形PMEF周长最小?请说明理由.
 |
 解:(1)设抛物线为
解:(1)设抛物线为
∵二次函数的图象过点A(-1,0)、C(0,5)
∴
解得:
∴二次函数的函数关系式为
即y=-x2+4x+5
(2)当a=1时,E(1,0),F(2,0),
设P的坐标为(x,-x2+4x+5)
过点P作y轴的垂线,垂足为G,
则四边形MEFP面积
=
=
=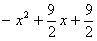
=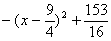
所以,当 时,四边形MEFP面积的最大,最大值为
时,四边形MEFP面积的最大,最大值为 ,
,
此时点P坐标为 .
.
 (3)EF=1,把点M向右平移1个单位得点M1,再做点M1关于x轴的对称点M2,在四边形FMEF中,因为边PM,EF为固定值,所以要使四边形FMEF周长最小,则ME+PF最小,因为ME=M1F=M2F,所以只要使M2F+PF最小即可,所以点F应该是直线M2P与x轴的交点,由OM=1,OC=5,得点P的纵坐标为3,根据y=-x2+4x+5可求得点P(
(3)EF=1,把点M向右平移1个单位得点M1,再做点M1关于x轴的对称点M2,在四边形FMEF中,因为边PM,EF为固定值,所以要使四边形FMEF周长最小,则ME+PF最小,因为ME=M1F=M2F,所以只要使M2F+PF最小即可,所以点F应该是直线M2P与x轴的交点,由OM=1,OC=5,得点P的纵坐标为3,根据y=-x2+4x+5可求得点P(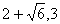 )
)
又点M2坐标为(1,-1),
所以直线M2P的解析式为: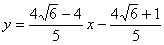 ,
,
当y=0时,求得 ,∴F(
,∴F( ,0)
,0)
∴


 所以,当
所以,当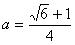 时,四边形FMEF周长最小.
时,四边形FMEF周长最小.


科目:初中数学 来源: 题型:
甲种污水处理器处理25吨的污水与乙种污水处理器处理35吨的污水所用时间相同,已知乙种污水处理器每小时比甲种污水处理器多处理20吨的污水,求两种污水处理器的污水处理效率.设甲种污水处理器的污水处理效率为x吨/小时,依题意列方程正确的是( )
A.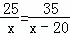 B.
B.  C.
C.  D.
D. 


查看答案和解析>>
科目:初中数学 来源: 题型:
四张扑克牌的牌面如图1,将扑克牌洗匀后,如图2背面朝上放置在桌面上,小明和小亮设计了A、B两种游戏方案:
方案A:随机抽一张扑克牌,牌面数字为5时小明获胜;否则小亮获胜.
方案B:随机同时抽取两张扑克牌,两张牌面数字之和为偶数时,小明获胜;否则小亮获胜.
请你帮小亮选择其中一种方案,使他获胜的可能性较大,并说明理由.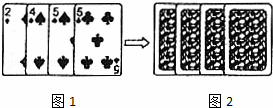


查看答案和解析>>
科目:初中数学 来源: 题型:
将抛物线y=x2平移得到抛物线y=(x+2)2,则这个平移过程正确的是( )
A.向左平移2个单位 B.向右平移2个单位
C.向上平移2个单位 D.向下平移2个单位
查看答案和解析>>
科目:初中数学 来源: 题型:
(1)解不等式组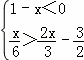 ,并把它的解集在数轴上表示出来.
,并把它的解集在数轴上表示出来.
(2)先阅读以下材料,然后解答问题,分解因式.
mx+nx+my+ny=(mx+nx)+(my+ny)=x(m+n)+y(m+n)=(m+n)(x+y);也可以mx+nx+my+ny=(mx+my)+(nx+ny)=m(x+y)+n(x+y)=(m+n)(x+y).以上分解因式的方法称为分组分解法,请用分组分解法分解因式:a3﹣b3+a2b﹣ab2.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com