
分析 (1)根据抛物线的顶点坐标及函数经过点(0,1),利用待定系数法求解即可.
(2)①先写出平移后的函数解析式,然后得出A、B、C三点的坐标,过点A作AH⊥BC于H,根据△ABC为等边三角形,可得出关于m的方程,解出即可;
②求出点D坐标,分两种情况进行讨论,①PD为对角线,②PD为边,根据菱形的性质求解即可.
解答 解:(1)由题意可得:$\left\{\begin{array}{l}a+b+c=0\\-\frac{b}{2a}=1\\ c=1.\end{array}\right.$,
解得:$\left\{\begin{array}{l}a=1\\ b=-2\\ c=1.\end{array}\right.$
∴抛物线对应的函数的解析式为y=x2-2x+1.
(2)①如图1: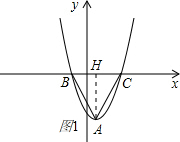
将y=x2-2x+1向下平移m个单位得:y=x2-2x+1-m=(x-1)2-m,
可知A(1,-m),B(1-$\sqrt{m}$,0),C(1+$\sqrt{m}$,0),BC=2$\sqrt{m}$.
过点A作AH⊥BC于H,
∵由△ABC为等边三角形,
∴BH=HC=$\frac{1}{2}$BC,∠CAH=30°,
∴AH=$\frac{HC}{tan∠CAH}$,即$\frac{\sqrt{m}}{\frac{\sqrt{3}}{3}}=m$,
由m>0,
解得:m=3.
②在抛物线上存在点P,能使四边形CBDP为菱形.理由如下:
∵点D与点A关于x轴对称,
∴D(1,3),
情况一:如图2,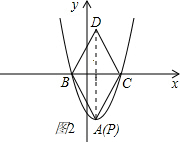
当DP为对角线时,显然点P在点A位置上时,符合题意,
故此时点P坐标为(1,-3);
情况二:当DP为边时要使四边形CBDP为菱形,需DP∥BC,DP=BC,如图3,
由点D的坐标为(1,3),DP=BC=2$\sqrt{3}$,可知点P的横坐标为1+2$\sqrt{3}$,
当x=1+2$\sqrt{3}$时,y=x2-2x+1-m=x2-2x-2=9≠3,
故不存在这样的点P.
综上可得,存在使四边形CBDP为菱形的点P,坐标为(1,-3).
点评 此题属于二次函数的综合题,属于综合性较强的题目,应理清思路,对每一个知识点都应熟练掌握并能灵活运用,求出二次函数的解析式是解此题的关键,应熟练掌握三点式和顶点式求抛物线解析式的方法,二次函数的平移通常指的是图象的平移,应注意总结平移的规律.


科目:初中数学 来源:2016-2017学年度海南省九年级第二次月考数学试卷(解析版) 题型:填空题
某校图书馆去年底有图书5万册,预计到明年年底增加到7.2万册,则这两年的年平均增长率为___________.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 各类 | 频数 | 频率 |
| 卡通画 | a | 0.56 |
| 时文杂志 | 32 | b |
| 武侠小说 | 30 | 0.15 |
| 文学名著 | c | d |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,点P、Q是反比例函数y=$\frac{k}{x}$(k≠0)图象上的两点,PA⊥y轴于点A,QN⊥x轴于点N,作PM⊥x轴于点M,QB⊥y轴于点B,连接PB、QM,记S△ABP=S1,S△QMN=S2,则S1与S2的大小关系为( )
如图,点P、Q是反比例函数y=$\frac{k}{x}$(k≠0)图象上的两点,PA⊥y轴于点A,QN⊥x轴于点N,作PM⊥x轴于点M,QB⊥y轴于点B,连接PB、QM,记S△ABP=S1,S△QMN=S2,则S1与S2的大小关系为( )| A. | S1>S2 | B. | S1<S2 | C. | S1=S2 | D. | 无法判定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
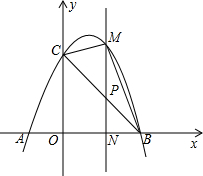 如图,已知抛物线y=-x2+2x+3与x轴交于A,B两点(点A在点B的左边),与y轴交于点C,连接BC.
如图,已知抛物线y=-x2+2x+3与x轴交于A,B两点(点A在点B的左边),与y轴交于点C,连接BC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com