
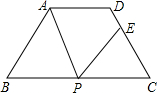
 如图,等腰梯形ABCD中,AD∥BC,AD=3,BC=7,∠B=60°,P为下底BC上一点(不与B、C重合),连结AP,过点P作PE交CD于E,使得∠APE=∠B
如图,等腰梯形ABCD中,AD∥BC,AD=3,BC=7,∠B=60°,P为下底BC上一点(不与B、C重合),连结AP,过点P作PE交CD于E,使得∠APE=∠B分析 (1)由等腰梯形ABCD中,AD∥BC,AB=CD,可得∠B=∠C=60°,又由∠APE+∠EPC=∠B+∠BAP,∠APE=∠B,可证得∠BAP=∠EPC,根据有两角对应相等的三角形相似,即可证得:△APB∽△PEC;
(2)作AF⊥BC,根据等腰梯形的性质求出BF的长,再由直角三角形的性质即可得出结论;
(3)根据DE:EC=5:3,CD=AB=4可得出DE=2.5,EC=1.5.再由△ABP∽△PCE可得出BP•PC=6,设BP=x,则x(7-x)=6,求出x的值即可.
解答 (1)证明:∵等腰梯形ABCD中,AD∥BC,AB=CD,
∴∠B=∠C=60°,
∵∠APC=∠B+∠BAP,
即∠APE+∠EPC=∠B+∠BAP,
∵∠APE=∠B,
∴∠BAP=∠EPC,
∴△APB∽△PEC
(2)解:作AF⊥BC, 则BF=$\frac{1}{2}$(BC-AD)=2,
则BF=$\frac{1}{2}$(BC-AD)=2,
∵∠B=60°,
∴∠BAF=30°,
∴AB=2BF=4;
(3)解:∵DE:EC=5:3,
∴DE=2.5,EC=1.5.
∵△ABP∽△PCE,
∴$\frac{AB}{\begin{array}{l}PC\end{array}}$=$\frac{BP}{CE}$,
∴$\frac{4}{PC}$=$\frac{BP}{1.5}$,
∴BP•PC=6
设BP=x,则x(7-x)=6
解得,x1=1,x2=6.
点评 此题考查的是四边形综合题,涉及到等腰梯形的性质、相似三角形的判定与性质以及等边三角形的判定与性质.此题难度适中,注意掌握辅助线的作法,注意数形结合思想与方程思想的应用.


 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:初中数学 来源: 题型:选择题
| A. | 连接两点的线段就是两点之间的距离 | |
| B. | 如果线段AB=AC,那么点A与点B的距离等于点A与点C的距离 | |
| C. | 连接两点的线段的长度,是两点间的距离 | |
| D. | 两点之间的距离是连接两点的所有线的长度中,长度最短的 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图,在正方形ABCD中,E为AD上一点,BF平分∠CBE交CD于F,若正方形边长为2$\sqrt{5}$,AE=4,求DF的长.
已知:如图,在正方形ABCD中,E为AD上一点,BF平分∠CBE交CD于F,若正方形边长为2$\sqrt{5}$,AE=4,求DF的长.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 在平面直角坐标系中,已知抛物线与直线的图象如图所示,当y1≠y2时,取y1,y2中的较大值记为N;当y1=y2时,N=y1=y2.则下列说法:
在平面直角坐标系中,已知抛物线与直线的图象如图所示,当y1≠y2时,取y1,y2中的较大值记为N;当y1=y2时,N=y1=y2.则下列说法:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
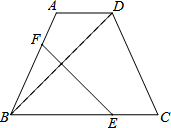 如图,在等腰梯形ABCD中,AD∥BC,∠ADB=45°,翻折梯形ABCD,使点B与点D重合,折痕分别交边AB、BC于点F、E,若AD=6,BC=14,那么cot∠C=$\frac{2}{5}$.
如图,在等腰梯形ABCD中,AD∥BC,∠ADB=45°,翻折梯形ABCD,使点B与点D重合,折痕分别交边AB、BC于点F、E,若AD=6,BC=14,那么cot∠C=$\frac{2}{5}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com