
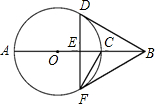
 (2007•海淀区二模)如图,AB经过⊙O的圆心,弦DF⊥AB于E,BF切⊙O于F,⊙O的半径为2.
(2007•海淀区二模)如图,AB经过⊙O的圆心,弦DF⊥AB于E,BF切⊙O于F,⊙O的半径为2. (1)证明:连接OD,OF.
(1)证明:连接OD,OF.| 3 |
| 3 |


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:初中数学 来源: 题型:
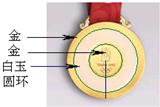 (2007•海淀区二模)北京奥运会金牌创造性地将白玉圆环嵌在其中(如图),这一设计不仅是对获胜者的礼赞,也形象地诠释了中华民族自古以来以“玉”比“德”的价值观.若白玉圆环面积与整个金牌面积的比值为k,则下列各数与k最接近的是( )
(2007•海淀区二模)北京奥运会金牌创造性地将白玉圆环嵌在其中(如图),这一设计不仅是对获胜者的礼赞,也形象地诠释了中华民族自古以来以“玉”比“德”的价值观.若白玉圆环面积与整个金牌面积的比值为k,则下列各数与k最接近的是( )查看答案和解析>>
科目:初中数学 来源: 题型:
 (2007•海淀区二模)用“¤”定义一种运算:对于任意实数m、n和抛物线y=ax2,当y=ax2¤(m,n)后都可得到y=a(x-m)2+n.例如:当y=3x2¤(2,4)后得到y=3(x-2)2+4.当函数y=x2¤(1,n)后得到了新函数的图象(如图所示),则n=
(2007•海淀区二模)用“¤”定义一种运算:对于任意实数m、n和抛物线y=ax2,当y=ax2¤(m,n)后都可得到y=a(x-m)2+n.例如:当y=3x2¤(2,4)后得到y=3(x-2)2+4.当函数y=x2¤(1,n)后得到了新函数的图象(如图所示),则n=查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com