练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

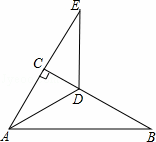
    如图，在Rt△ABC中，∠ACB=90°，∠B=30°，AD平分∠CAB．

    （1）求∠CAD的度数；

    （2）延长AC至E，使CE=AC，求证：DA=DE．


    （1）解：如图，∵在Rt△ABC中，∠ACB=90°，∠B=30°，

    ∴∠B=30°，

    ∴∠CAB=60°．

    又∵AD平分∠CAB，

    ∴∠CAD=∠CAB=30°，即∠CAD=30°；

    （2）证明：∵∠ACD+∠ECD=180°，且∠ACD=90°，

    ∴∠ECD=90°，

    ∴∠ACD=∠ECD．

    在△ACD与△ECD中，，

    ∴△ACD≌△ECD（SAS），

    ∴DA=DE．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    下列运算正确的是（　　）

    　   A．                       a3•a2=a5                       B．                             a6÷a2=a3   C． （a3）2=a5     D． （3a）3=3a3

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    分解因式：a2b﹣b3=　        

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知三角形两边长分别为3和8，则该三角形第三边的长可能是（　　）

    　

    A．

    5

    B．

    10

    C．

    11

    D．

    12

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在4×4的正方形网格中，每个小正方形的边长为1，若将△AOC绕点O顺时针旋转90°得到△BOD，则的长为（　　）

    　

    A．

    π

    B．

    6π

    C．

    3π

    D．

    1.5π

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    在矩形ABCD中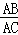，=a，点G，H分别在边AB，DC上，且HA=HG，点E为AB边上的一个动点，连接HE，把△AHE沿直线HE翻折得到△FHE．

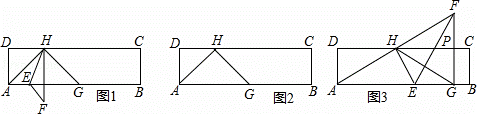
    （1）如图1，当DH=DA时，

    ①填空：∠HGA=　45　度；

    ②若EF∥HG，求∠AHE的度数，并求此时的最小值；

    （2）如图3，∠AEH=60°，EG=2BG，连接FG，交边FG，交边DC于点P，且FG⊥AB，G为垂足，求a的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    若一个正n边形的每个内角为156°，则这个正n边形的边数是（　　）

    　

    A．

    13

    B．

    14

    C．

    15

    D．

    16

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图1，在⊙O中，E是弧AB的中点，C为⊙O上的一动点（C与E在AB异侧），连接EC交AB于点F，EB=（r是⊙O的半径）．

    （1）D为AB延长线上一点，若DC=DF，证明：直线DC与⊙O相切；

    （2）求EF•EC的值；

    （3）如图2，当F是AB的四等分点时，求EC的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    在一个不透明的口袋中，有四个完全相同的小球，把它们分别标号为1、2、3、4，随机地摸取一个小球记下标号后放回，再随机地摸取一个小球记下标号，则两次摸取的小球标号都是1的概率为　　．

    查看答案和解析>>

    同步练习册答案