
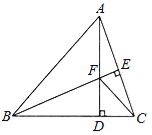
【题目】如图,在△ABC中,AB=BC,BE⊥AC于点E,AD⊥BC于点D,
∠BAD=45°,AD与BE交于点F,连接CF.

(1)求证:BF=2AE;
(2)若CD=![]() ,求AD的长.
,求AD的长.
【答案】(2)2+![]()
【解析】试题分析:(1)先判定出△ABD是等腰直角三角形,根据等腰直角三角形的性质可得AD=BD,再根据同角的余角相等求出∠CAD=∠CBE,然后利用“角边角”证明△ADC和△BDF全等,根据全等三角形对应边相等可得BF=AC,再根据等腰三角形三线合一的性质可得AC=2AE,从而得证;
(2)根据全等三角形对应边相等可得DF=CD,然后利用勾股定理列式求出CF,再根据线段垂直平分线上的点到线段两端点的距离相等可得AF=CF,然后根据AD=AF+DF代入数据即可得解.
(1)证明:∵AD⊥BC,∠BAD=45°,
∴△ABD是等腰直角三角形,
∴AD=BD,
∵BE⊥AC,AD⊥BC
∴∠CAD+∠ACD=90°,
∠CBE+∠ACD=90°,
∴∠CAD=∠CBE,
在△ADC和△BDF中,![]() ,
,
∴△ADC≌△BDF(ASA),
∴BF=AC,
∵AB=BC,BE⊥AC,
∴AC=2AE,
∴BF=2AE;
(2)解:∵△ADC≌△BDF,
∴DF=CD=,
在Rt△CDF中,CF=![]() =
=![]() =2,
=2,
∵BE⊥AC,AE=EC,
∴AF=CF=2,
∴AD=AF+DF=2+.


 步步高达标卷系列答案
步步高达标卷系列答案科目:初中数学 来源: 题型:
【题目】甲、乙两人在5次打靶测试中命中的环数如下:
甲:8,8,7,8,9;乙:5,9,7,10,9.
(1)填写下表:

(2)教练根据这5次成绩,选择甲参加射击比赛,教练的理由是什么?
(3)如果乙再射击1次,命中8环,那么乙的射击成绩的方差如何变化?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了调查学生每天零花钱情况,对我校初二学年某班 50 名同学每天零花钱情况进行 了统计,并绘制成下面的统计图.
(1)直接写出这 50 名同学零花钱数据的众数是_____;中位数是________.
(2)求这 50 名同学零花钱的平均数.
(3)该校共有学生 3100 人,请你根据该班的零花钱情况,估计这个中学学生每天的零花 钱不小于 30 元的人数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=8cm,BC=6cm,CD⊥AB于D,求:

(1)斜边AB的长;
(2)△ABC的面积;
(3)高CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在笔直的铁路上A、B两点相距25km,C、D为两村庄,DA=10km,CB=15km,DA⊥AB于A,CB⊥AB于B,现要在AB上建一个中转站E,使得C、D两村到E站的距离相等.求E应建在距A多远处?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中,已知点O(0,0),A(1,0),B(1,1),C(2,0),△OBC的面积记为S1 , 过O、B、C三点的半圆面积记为S2;过O、B、C三点的抛物线与x轴所围成的图形面积记为S3 , 则S1、S2、S3的大小关系是 . (用“>”连接)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是正方形ABCD内一点,点P到点A、B和D的距离分别为1,2 ![]() ,
, ![]() ,△ADP沿点A旋转至△ABP′,连结PP′,并延长AP与BC相交于点Q.
,△ADP沿点A旋转至△ABP′,连结PP′,并延长AP与BC相交于点Q. 
(1)求证:△APP′是等腰直角三角形;
(2)求∠BPQ的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为提倡节约用水,准备实行自来水“阶梯计费”方式,用户用水不超出基本用水量的部分享受基本价格,超出基本用水量的部分实行加价收费,为更好地做决策,自来水公司随机抽取部分用户的用水量数据,并绘制了如图不完整的统计图(每组数据包括最大值但不包括最小值),请你根据统计图解决下列问题:
(1)此次抽样调查的样本容量是
(2)补全左侧统计图,并求扇形统计图中“25吨~30吨”部分的圆心角度数.
(3)如果自来水公司将基本用水量定为每户25吨,那么该地区6万用户中约有多少用户的用水全部享受基本价格?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com