
分析 (1)根据长方形的周长公式即可求出答案.
(2)根据长方形的面积公式即可求出面积,从而可求出正方形的边长;
(3)根据(1)和(2)的计算结果即可找出规律.
(4)可从正方形的对角线或长方形的对角线进行考虑.
解答 解:(1)长方形的周长为:2(a+b)=$\sqrt{32}$+$\frac{2}{3}$$\sqrt{18}$=6$\sqrt{2}$
(2)长方形的面积为:$\frac{1}{2}$$\sqrt{32}$×$\frac{1}{3}$$\sqrt{18}$=4,
∴正方形的面积为4,
∴正方形的边长为2,
∴正方形的周长为2×4=8;
(3)由上面计算可知:若长方形的面积为:ab=4,另一个正方形,其面积与该长方形面积相等时,
周长为该长方形面积的2倍;
(4)可从正方形的对角线或长方形的对角线进行考虑.答案不唯一.
点评 本题考查二次根式的应用,解题的关键是熟练运用二次根式的性质,本题属于基础题型.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:填空题
 如图,在直角坐标系中,△ABC的面积为2,三个顶点的坐标分别为A(3,2),B(1,1),C(a,b),且a、b均为正整数,则C点的坐标为(5,1),(1,3),(3,4),(5,5).
如图,在直角坐标系中,△ABC的面积为2,三个顶点的坐标分别为A(3,2),B(1,1),C(a,b),且a、b均为正整数,则C点的坐标为(5,1),(1,3),(3,4),(5,5).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
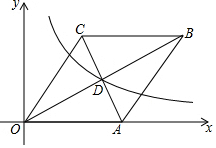 如图,在平面直角坐标系中,菱形OABC的边OA在x轴上,AC与OB交于点D (8,4),反比例函数y=$\frac{k}{x}$的图象经过点D.若将菱形OABC向左平移n个单位,使点C落在该反比例函数图象上,则n的值为2.
如图,在平面直角坐标系中,菱形OABC的边OA在x轴上,AC与OB交于点D (8,4),反比例函数y=$\frac{k}{x}$的图象经过点D.若将菱形OABC向左平移n个单位,使点C落在该反比例函数图象上,则n的值为2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
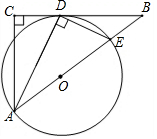 已知:如图,在△ABC中,∠C=90°,∠BAC的平分线AD交BC于点D,过点D作DE⊥AD交AB于点E,以AE为直径作⊙O.
已知:如图,在△ABC中,∠C=90°,∠BAC的平分线AD交BC于点D,过点D作DE⊥AD交AB于点E,以AE为直径作⊙O.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
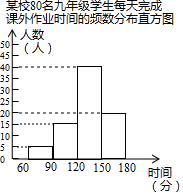 为了解九年级课业负担情况,某校随机抽取80名九年级学生进行问卷调查,在整理并汇总这80张有效问卷的数据时发现,每天完成课外作业时间,最长不超过180分钟,最短不少于60分钟,并将调查结果绘制成如图所示的频数分布直方图.
为了解九年级课业负担情况,某校随机抽取80名九年级学生进行问卷调查,在整理并汇总这80张有效问卷的数据时发现,每天完成课外作业时间,最长不超过180分钟,最短不少于60分钟,并将调查结果绘制成如图所示的频数分布直方图.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com