
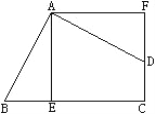
【题目】如图,四边形ABCD的∠BAD=∠C=90,AB=AD,AE⊥BC于E,![]() 旋转后能与
旋转后能与![]() 重合.
重合.
(1)旋转中心是哪一点?
(2)旋转了多少度?
(3)若AE=5㎝,求四边形AECF的面积.
【答案】
【1】 点A;
【2】 90度
【3】 25cm2
【解析】
试题(1)旋转中心到对应点的距离相等,因为AB=AD,AE=AF,所以点O是对称中心.而对应线段AB,AD和夹角∠BAD=90°,对应线段AE,AF的夹角∠EAF=90°,所以旋转的角度是90°;
(2)当把△ABE旋转到△ADF的位置后,四边形ABCD就变化为四边形AECF,由题意可得到四边形AECF是正方形,从而由四边形AECF的面积得到四边形ABCD的面积.
试题解析:(1)旋转中心是点A,因为∠BAD=90°,所以旋转了90°.
答:旋转中心是点A,旋转了90°.
(2)因为△BEA≌△DFA,所以AE=AF,∠EAB=∠FAD,而∠BAD=90°,
所以∠EAF=90°,又∠AEC=90°,∠C=90°,
所以四边形AECF是正方形,
因为AE=5,所以正方形AECF的面积为:5×5=25 cm2.
又因为△BEA≌△DFA,所以四边形ABCD的面积是25 cm2.
答:四边形ABCD的面积是25 cm2.


科目:初中数学 来源: 题型:
【题目】如图,已知一次函数![]() 的图象与x轴、y轴分别交于
的图象与x轴、y轴分别交于![]() 两点,与反比例函数
两点,与反比例函数![]() 的图象分别交于
的图象分别交于![]() 两点,点
两点,点![]() ,
,![]() .
.
![]() 求一次函数
求一次函数![]() 与反比例函数
与反比例函数![]() 的解析式;
的解析式;
![]() 直接写出
直接写出![]() 时自变量x的取值范围.
时自变量x的取值范围.
![]() 动点
动点![]() 在y轴上运动,当
在y轴上运动,当![]() 的值最大时,直接写出P点的坐标.
的值最大时,直接写出P点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC绕点C顺时针旋转90°得到△EDC.若点A,D,E在同一条直线上,∠ACB=20°,则∠ADC的度数是( )

A. 55° B. 60° C. 65° D. 70°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为改善交通拥堵状况,我市进行了大规模的道路桥梁建设.已知某路段乙工程队单独完成所需的天数是甲工程队单独完成所需天数的1.5倍,如果按甲工程队单独工作20天,再由乙工程队单独工作30天的方案施工,这样就完成了此路段的![]() .
.
(1)求甲、乙工程队单独完成这项工程各需多少天?
(2)已知甲工程队每天的施工费用是2万元,乙工程队每天的施工费用为1.2万元,要使该项目的工程费不超过114万元,则需要改变施工方案,但甲乙两个工程队不能同时施工,乙工程队最少施工多少天才能完成此项工程?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,己知O为坐标原点,点A(3,0),B(0.4),以点A为旋转中心,把△ABO顺时针旋转,得△ACD.记旋转角为α.∠ABO为β.

(I )如图①,当旋转后点D恰好落在AB边上时,求点D的坐标;
(II)如图②,当旋转后满足BC∥x轴时,求α与β之间的数量关系:
(III)当旋转后满足∠AOD=β时,求直线CD的解析式(直接写出结果即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正五边形ABCDE内接于⊙O,过点A作⊙O的切线交对角线DB的延长线于点F,则下列结论不成立的是( )
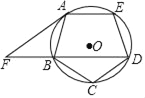
A. AE∥BD B. AB=BF C. AF∥CD D. DF=![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】作图题:

(1)如图①,已知:![]() .求作:射线
.求作:射线![]() ,使
,使![]() 平分
平分![]() .(要求:尺规作图,不写作法,但需保留作图痕迹) .
.(要求:尺规作图,不写作法,但需保留作图痕迹) .
(2)题(1)中作图的依据是全等三角形判定方法中的__________.
(3)在图②中作出![]() ,使它与
,使它与![]() 关于
关于![]() 轴对称.
轴对称.
(4)在图②中的![]() 轴上找到一点
轴上找到一点![]() ,使
,使![]() 的周长最小.
的周长最小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC和∠ACB的平分线相交于点P,根据下列条件,求∠BPC的度数.
(1)若∠ABC=50°,∠ACB=60°,则∠BPC= ;
(2)若∠ABC+∠ACB=120°,则∠BPC= ;
(3)若∠A=80°,则∠BPC= ;
(4)从以上的计算中,你能发现已知∠A,求∠BPC的公式是:∠BPC= (提示:用∠A表示).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com