6．问题提出：我们知道，等式具有性质：（1）等式两边同时加或减同一个代数式，所得结果仍是等式；（2）等式两边同时乘同一个数或除以同一个不为0的数，所得结果仍是等式．那么任意 一个三阶幻方是否也有类似的性质？
问题探究：为了探究上述问题，我们不妨从简单的三阶幻方①入手；
探究一
如图②，九个数2，3，4，5，6，7，8，9，10已填到方格中，显然每行、每列、每条对角线上的三个数之和都相等，构成了一个三阶幻方②，所以构成三阶幻方①的九个数同时加1，所得到的九个数仍可构成一个三阶幻方．
如图③，九个数-2，-1，0，1，2，3，4，5，6已填到方格中，显然每行、每列、每条对角线上的三个数之和都相等，构成了一个三阶幻方③，所以构成三阶幻方①的九个数同时减3，所得到的九个数仍可构成一个三阶幻方．
请把九个数0.5，1.5，2.5，3.5，4.5，5.5，6.5，7.5，8.5填到图④的方格中，使得每行、每列、每条对角线上的三个数之和都相等，构成了一个三阶幻方④，所以构成三阶幻方①的九个数同时减0.5，所得到的九个数仍可构成一个三阶幻方．
1．根据探究一可得任意三阶幻方的性质（1）：构成三阶幻方的九个数，每个数同时加或减同一个数，所得到的九个数仍能构成三阶幻方．
探究二：
如图⑤，九个数3，6，9，12，15，18，21，24，27已填到方格中，显然每行、每列、每条对角线上的三个数之和都相等，构成了一个三阶幻方⑤．所以构成三阶幻方①的九个数同时乘3，所得到的九个数仍可构成一个三阶幻方．
如图⑥，九个数0.5，1，1.5，2，2.5，3，3.5，4，4.5已填到方格中，显然每行、每列、每条对角线上的三个数之和都相等，构成了一个三阶幻方⑥．所以构成三阶幻方①的九个数同时除以2，所得到的九个数仍可构成一个三阶幻方．
请把九个数-2，-4，-6，-8，-10，-12，-14，-16，-18填到图⑦的方格中，使得每行、每列、每条对角线上的三个数之和都相等，构成了一个三阶幻方⑦．所以构成三阶幻方①的九个数同时乘-2，所得到的九个数仍可构成一个三阶幻方．
2．根据探究二可得任意三阶幻方的性质（2）：构成三阶幻方的九个数，每个数同时乘同一个数或除以同一个不为0的数，所得到的九个数仍能构成三阶幻方．．
性质应用：
3，5，7，9，11，13，15，17，19这九个数能否构成三阶幻方？请用三阶幻方的性质进行说明．
阅读快车系列答案
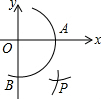如图，在平面直角坐标系中，以点O为圆心，适当的长为半径画弧，交x轴于点A，交y轴于点B，再分别以点A，B为圆心，大于$\frac{1}{2}$AB的长为半径画弧，两弧在第四象限交于点P．若点P的坐标为（2a，a-9），则a的值为3．
如图，BD=CD，DE⊥AB，DF⊥AC，DE=DF，∠A=90°，试说明：AB=AC．