
如图,东西方向上的A,B两座城市相距100千米,现计划在这两座城市之间修筑一条高等级公路(即线段AB),经测量,森林保护区中心P点在A城市的北偏东![]() 方向,B城市的北偏西
方向,B城市的北偏西![]() 方向上.已知森林保护区的范围在以P为圆心,50千米为半径的圆形区域内,请问,计划修筑的这条高等级公路会不会穿越保护区?为什么?
方向上.已知森林保护区的范围在以P为圆心,50千米为半径的圆形区域内,请问,计划修筑的这条高等级公路会不会穿越保护区?为什么?

|
[答案]过P作PC⊥AB于C,设PC=x千米,则在Rt△APC中, ∵PC∥AE,∴∠APC=∠EAP= 在Rt△BPC中,∵PC∥BF,∴∠BPC= ∴BC=PC·tan∠BPC=x ∴AB= ∴x= ∵PC=63.4>50, ∴计划修筑的这条高等级公路不会穿越保护区. [剖析]过P作PC⊥AB,则PC的长即是P到AB的最短距离,这个距离比50千米大,说明AB不会穿越保护区. |
|
[拓展延伸] 类似于本题这样的问题,其实质是求点到直线的距离.常规辅助线是过这点作已知直线的垂线段,求出垂线段的长后,再和限制距离比较大小,如本题是通过比较点P到AB的距离与限制距离50比较大小,从而解决问题. |


科目:初中数学 来源: 题型:填空题
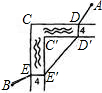 如图,护城河在CC'处直角转弯,宽度保持为4米.从A处往B处,经过2座桥:DD',EE'.设护城河是东西一南北方向的,A、B在东西方向上相距64米,南北方向上相距84米.恰当地架桥可使AD、D'E′、EB的路程最短.这个最短路程为________米.
如图,护城河在CC'处直角转弯,宽度保持为4米.从A处往B处,经过2座桥:DD',EE'.设护城河是东西一南北方向的,A、B在东西方向上相距64米,南北方向上相距84米.恰当地架桥可使AD、D'E′、EB的路程最短.这个最短路程为________米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,荆州古城河在CC′处直角转弯,河宽均为5米,从A处到达B处,须经两座桥:DD′,EE′(桥宽不计),设护城河以及两座桥都是东西、南北方向的,A、B在东西方向上相距65米,南北方向上相距85米,恰当地架桥可使ADD′E′EB的路程最短,这个最短路程是多少米?
如图,荆州古城河在CC′处直角转弯,河宽均为5米,从A处到达B处,须经两座桥:DD′,EE′(桥宽不计),设护城河以及两座桥都是东西、南北方向的,A、B在东西方向上相距65米,南北方向上相距85米,恰当地架桥可使ADD′E′EB的路程最短,这个最短路程是多少米?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com