
 用19米长的铝合金条制成如图所示的矩形窗框,CD长表示窗框的宽,EF=0.5米.(铝合金条的宽度忽略不计)
用19米长的铝合金条制成如图所示的矩形窗框,CD长表示窗框的宽,EF=0.5米.(铝合金条的宽度忽略不计)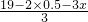 =6-x,AC=BC+AB,
=6-x,AC=BC+AB, .
. )x=-x 2+
)x=-x 2+ x,
x, x,
x, =-
=-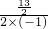 =
= 时,
时, =
=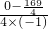 =
=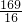 ;
; )x=10,
)x=10,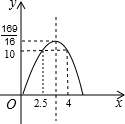
 ,x2=4,
,x2=4, x,
x, ,
,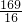 ),
),

 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源: 题型:
 (2011•南岗区一模)用19米长的铝合金条制成如图所示的矩形窗框ACDF.其中BE、GH均是铝合金制成的格条,且BE∥AF,GH⊥CD,EF=0.5m.设AF的长为x(单位:米),AC的长为y(单位:米).
(2011•南岗区一模)用19米长的铝合金条制成如图所示的矩形窗框ACDF.其中BE、GH均是铝合金制成的格条,且BE∥AF,GH⊥CD,EF=0.5m.设AF的长为x(单位:米),AC的长为y(单位:米).查看答案和解析>>
科目:初中数学 来源: 题型:
 用19米长的铝合金条制成如图所示的矩形窗框,CD长表示窗框的宽,EF=0.5米.(铝合金条的宽度忽略不计)
用19米长的铝合金条制成如图所示的矩形窗框,CD长表示窗框的宽,EF=0.5米.(铝合金条的宽度忽略不计)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 用19米长的铝合金条制成如图所示的矩形窗框ACDF.其中BE、GH均是铝合金制成的格条,且BE∥AF,GH⊥CD,EF=0.5m.设AF的长为x(单位:米),AC的长为y(单位:米).
用19米长的铝合金条制成如图所示的矩形窗框ACDF.其中BE、GH均是铝合金制成的格条,且BE∥AF,GH⊥CD,EF=0.5m.设AF的长为x(单位:米),AC的长为y(单位:米).查看答案和解析>>
科目:初中数学 来源:2011年黑龙江省哈尔滨市南岗区中考数学一模试卷(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com