
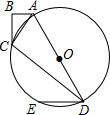
 如图,在四边形ABCD中,AB=6,BC=8,CD=24,AD=26,∠B=90°,以AD为直径作圆O,过点D作DE∥AB交圆O于点E
如图,在四边形ABCD中,AB=6,BC=8,CD=24,AD=26,∠B=90°,以AD为直径作圆O,过点D作DE∥AB交圆O于点E分析 (1)如图1,连结CO.先由勾股定理求出AC=10,再利用勾股定理的逆定理证明△ACD是直角三角形,∠C=90°,那么OC为Rt△ACD斜边上的中线,根据直角三角形斜边上的中线等于斜边的一半得出OC=$\frac{1}{2}$AD=r,即点C在圆O上;
(2)如图2,延长BC、DE交于点F,∠BFD=90°.根据同角的余角相等得出∠CDE=∠ACB.在Rt△ABC中,利用正切函数定义求出tan∠ACB=$\frac{6}{8}$=$\frac{3}{4}$,则tan∠CDE=tan∠ACB=$\frac{3}{4}$;
(3)如图3,连结AE,作OG⊥ED于点G,则OG∥AE,且OG=$\frac{1}{2}$AE.易证△ABC∽△CFD,根据相似三角形对应边成比例求出CF=$\frac{72}{5}$,那么BF=BC+CF=$\frac{112}{5}$.再证明四边形ABFE是矩形,得出AE=BF=$\frac{112}{5}$,所以OG=$\frac{1}{2}$AE=$\frac{56}{5}$.
解答 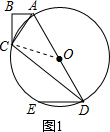 (1)证明:如图1,连结CO.
(1)证明:如图1,连结CO.
∵AB=6,BC=8,∠B=90°,
∴AC=10.
又∵CD=24,AD=26,102+242=262,
∴△ACD是直角三角形,∠ACD=90°.
∵AD为⊙O的直径,
∴AO=OD,OC为Rt△ACD斜边上的中线,
∴OC=$\frac{1}{2}$AD=r,
∴点C在圆O上;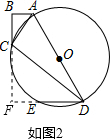 (2)解:如图2,延长BC、DE交于点F,∠BFD=90°.
(2)解:如图2,延长BC、DE交于点F,∠BFD=90°.
∵∠BFD=90°,
∴∠CDE+∠FCD=90°,
又∵∠ACD=90°,
∴∠ACB+∠FCD=90°,
∴∠CDE=∠ACB.
在Rt△ABC中,tan∠ACB=$\frac{6}{8}$=$\frac{3}{4}$,
∴tan∠CDE=tan∠ACB=$\frac{3}{4}$;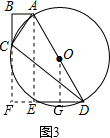 (3)解:如图3,连结AE,作OG⊥ED于点G,则OG∥AE,且OG=$\frac{1}{2}$AE.
(3)解:如图3,连结AE,作OG⊥ED于点G,则OG∥AE,且OG=$\frac{1}{2}$AE.
易证△ABC∽△CFD,
∴$\frac{AB}{CF}$=$\frac{AC}{CD}$,即$\frac{6}{CF}$=$\frac{10}{24}$,
∴CF=$\frac{72}{5}$,
∴BF=BC+CF=8+$\frac{72}{5}$=$\frac{112}{5}$.
∵∠B=∠F=∠AED=90°,
∴四边形ABFE是矩形,
∴AE=BF=$\frac{112}{5}$,
∴OG=$\frac{1}{2}$AE=$\frac{56}{5}$,
即圆心O到弦ED的距离为$\frac{56}{5}$.
点评 本题是圆的综合题,考查了勾股定理及其逆定理,直角三角形的性质,余角的性质,锐角三角函数定义,相似三角形的判定与性质,综合性较强,难度适中.准确作出辅助线,利用数形结合是解题的关键.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2000(22-x)=2×1200x | B. | 2×2000(22-x)=1200x | ||
| C. | 1200(22-x)=2×2000x | D. | 2×1200(22-x)=2000x |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
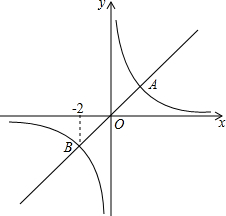 正比例函数y1=k1x的图象与反比例函数y2=$\frac{{k}_{2}}{x}$的图象相交于A,B两点,其中点B的横坐标为-2,当y1<y2时,x的取值范围是( )
正比例函数y1=k1x的图象与反比例函数y2=$\frac{{k}_{2}}{x}$的图象相交于A,B两点,其中点B的横坐标为-2,当y1<y2时,x的取值范围是( )| A. | x<-2或x>2 | B. | x<-2或0<x<2 | C. | -2<x<0或0<x<2 | D. | -2<x<0或x>2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com