
 某海域有A、B两个港口,B港口在A港口北偏西30°方向上,距A港口60海里,有一艘船从A港口出发,沿东北方向行驶一段距离后,到达位于B港口南偏东75°方向的C处,求:
某海域有A、B两个港口,B港口在A港口北偏西30°方向上,距A港口60海里,有一艘船从A港口出发,沿东北方向行驶一段距离后,到达位于B港口南偏东75°方向的C处,求:分析 (1)由平行线的性质以及方向角的定义得出∠FBA=∠EAB=30°,∠FBC=75°,那么∠ABC=45°,又根据方向角的定义得出∠BAC=∠BAE+∠CAE=75°,利用三角形内角和定理求出∠C=60°;
(2)作AD⊥BC交BC于点D,解Rt△ABD,得出BD=AD=30$\sqrt{2}$,解Rt△ACD,得出CD=$\frac{30\sqrt{2}}{\sqrt{3}}$=10$\sqrt{6}$,那么BC=BD+CD=30$\sqrt{2}$+10$\sqrt{6}$.
解答 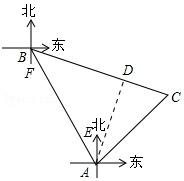 解:(1)如图,∵∠EAB=30°,AE∥BF,
解:(1)如图,∵∠EAB=30°,AE∥BF,
∴∠FBA=30°,又∠FBC=75°,
∴∠ABC=45°,
又∵∠BAC=∠BAE+∠CAE=75°,
∴∠C=60°.
故答案为60;
(2)如图,作AD⊥BC于D,
在Rt△ABD中,∵∠ABD=45°,AB=60,
∴AD=BD=30$\sqrt{2}$.
在Rt△ACD中,∵∠C=60°,AD=30$\sqrt{2}$,
∴tanC=$\frac{AD}{CD}$,
∴CD=$\frac{30\sqrt{2}}{\sqrt{3}}$=10$\sqrt{6}$,
∴BC=BD+CD=30$\sqrt{2}$+10$\sqrt{6}$.
答:该船与B港口之间的距离CB的长为(30$\sqrt{2}$+10$\sqrt{6}$)海里.
点评 本题考查的是解直角三角形的应用-方向角问题,平行线的性质,三角形内角和定理,构造直角三角形,利用三角函数求出线段BD与CD的长度是解题的关键.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:初中数学 来源: 题型:填空题
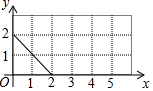 如图,动点P从(0,2)出发,沿所示的方向在矩形网格中运动,每当碰到矩形的边时反弹,反弹时反射角等于入射角,若第一次碰到矩形的边时坐标为P1(2,0),则P2017的坐标为(2,0).
如图,动点P从(0,2)出发,沿所示的方向在矩形网格中运动,每当碰到矩形的边时反弹,反弹时反射角等于入射角,若第一次碰到矩形的边时坐标为P1(2,0),则P2017的坐标为(2,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m2•n2=(mn)4 | B. | 5x2y-4x2y=1 | C. | m-2=$\frac{1}{{m}^{2}}$(m≠0) | D. | (m-n)2=m2-n2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
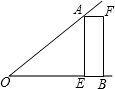 如图,已知∠AOB,OA=OB,点E在OB 上,四边形AEBF是矩形.
如图,已知∠AOB,OA=OB,点E在OB 上,四边形AEBF是矩形.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com