
【题目】如图,等腰![]() 与等腰
与等腰![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,垂足为
,垂足为![]() ,直线
,直线![]() 交
交![]() 于点
于点![]() .将
.将![]() 绕点
绕点![]() 顺时针旋转,则
顺时针旋转,则![]() 的长的最大值是______.
的长的最大值是______.

【答案】![]()
【解析】
延长ED到N,使得DN=DE,连接CN,BN,延长BN交AE于M.取BC的中点F,连接AF,OF.利用矩形的性质证明OD∥BN,推导出OB=OE,求出OF,AF即可解决问题.
如图,延长ED到N,使得DN=DE,连接CN,BN,延长BN交AE于M.取BC的中点F,连接AF,OF.
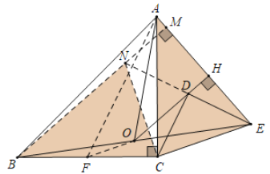
∵CD⊥EN,DN=DE,
∴CN=CE,
∵DC=DE,∠CDE=90°,
∴∠DCE=∠DCN=45°,
∴∠ACB=∠NCE=90°,
∴∠BCN=∠ACE,
在△BCN和△ACE中,
 ,
,
∴△BCN≌△ACE(SAS),
∴∠BNC=∠AEC,
∵∠BNC+∠CNM=180°,
∴∠CNM+∠AEC=180°,
∴∠ECN+∠NME=180°,
∵∠ECN=90°,
∴∠NME=90°,
∵DH⊥AE,
∴∠NME=∠DHE=90°,
∴OD∥BN,
∵DN=DE,
∴OB=OE,
∵BF=CF,
∴OF=![]() EC,
EC,
∵CD=DE=6,∠CDE=90°,
∴EC=6![]() ,
,
∴OF=3![]() ,
,
在Rt△ACF中,∵AC=12,CF=6,
∴![]() ,
,
∵OA≤AF+OF,
∴OA≤6![]() +3
+3![]() ,
,
∴OA的最大值为6![]() +3
+3![]() .
.
故答案为6![]() +3
+3![]() .
.


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:
【题目】如图,点A是以BC为直径的半圆的中点,连接AB,点D是直径BC上一点,连接AD,分别过点B、点C向AD作垂线,垂足为E和F,其中,EF=2,CF=6,BE=8,则AB的长是( )

A.4B.6C.8D.10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,旗杆及升旗台的剖面和教学楼的剖面在同一平面上,旗杆与地面垂直,在教学楼底部E点处测得旗杆顶端的仰角∠AED=58°,升旗台底部到教学楼底部的距离DE=7米,升旗台坡面CD的坡度i=1:0.75,坡长CD=2米,若旗杆底部到坡面CD的水平距离BC=1米,求旗杆AB的高度约为多少?(保留一位小数,参考数据:sin58°≈0.85,cos58°≈0.53,tan58°≈1.6)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 的两直角边
的两直角边![]() ,
,![]() 分别在
分别在![]() 轴的负半轴和
轴的负半轴和![]() 轴的正半轴上,
轴的正半轴上,![]() 为坐标原点,
为坐标原点,![]() ,
,![]() 两点的坐标分别为
两点的坐标分别为![]() 、
、![]() ,抛物线
,抛物线![]() 经过点
经过点![]() ,且顶点在直线
,且顶点在直线![]() 上.
上.

(1)求抛物线对应的函数关系式;
(2)若![]() 是由
是由![]() 沿
沿![]() 轴向右平移得到的,当四边形
轴向右平移得到的,当四边形![]() 是菱形时,试判断点
是菱形时,试判断点![]() 和点
和点![]() 是否在该抛物线上,并说明理由;
是否在该抛物线上,并说明理由;
(3)在(2)的条件下,若![]() 点是
点是![]() 所在直线下方抛物线上的一个动点,过点
所在直线下方抛物线上的一个动点,过点![]() 作
作![]() 平行于
平行于![]() 轴交
轴交![]() 于
于![]() .设点
.设点![]() 的横坐标为
的横坐标为![]() ,
,![]() 的长度为
的长度为![]() .求
.求![]() 与
与![]() 之间的函数关系式,写出自变量
之间的函数关系式,写出自变量![]() 的取值范围,并求
的取值范围,并求![]() 取最大值时,点
取最大值时,点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 交
交![]() 轴于
轴于![]() ,
,![]() 两点(点
两点(点![]() 在点
在点![]() 的左边),交
的左边),交![]() 轴正半轴于点
轴正半轴于点![]() .
.
(1)如图1,当![]() 时.
时.
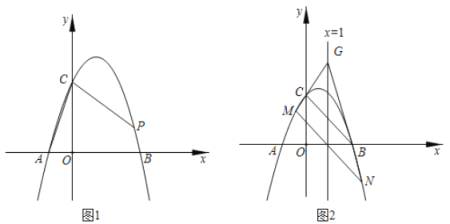
①直接写出点![]() ,
,![]() ,
,![]() 的坐标;
的坐标;
②若抛物线上有一点![]() ,使
,使![]() ,求点
,求点![]() 的坐标.
的坐标.
(2)如图2,平移直线![]() 交抛物线于
交抛物线于![]() ,
,![]() 两点,直线
两点,直线![]() 与直线
与直线![]() 交于点
交于点![]() ,若点
,若点![]() 在定直线
在定直线![]() 上运动,求
上运动,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
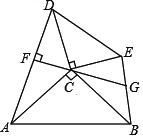
【题目】如图,点 C 为 Rt△ACB 与 Rt△DCE 的公共点,∠ACB=∠DCE=90°,连 接 AD、BE,过点 C 作 CF⊥AD 于点 F,延长 FC 交 BE 于点 G.若 AC=BC=25,CE=15, DC=20,则![]() 的值为___________.
的值为___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场要经营一种新上市的文具,进价为20元,试营销阶段发现:当销售单价是25元时,每天的销售量为250件,销售单价每上涨1元,每天的销售量就减少10件.
(1)写出商场销售这种文具,每天所得的销售利润![]() (元)与销售单价
(元)与销售单价![]() (元)之间的函数关系式;
(元)之间的函数关系式;
(2)求销售单价为多少元时,该文具每天的销售利润最大;最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
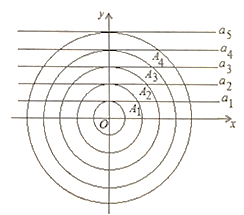
【题目】如图所示,在平面直角坐标系中,一组同心圆的圆心为坐标原点![]() ,它们的半径分别为
,它们的半径分别为![]() .按照“加
.按照“加![]() "依次递增; 一组平行线
"依次递增; 一组平行线![]() , ..分别过
, ..分别过![]() ,且与过该点的圆相切.若半径为
,且与过该点的圆相切.若半径为![]() 的圆与
的圆与![]() 在第一象限内交于点
在第一象限内交于点![]() ,半径为
,半径为![]() 的圆与
的圆与![]() 在第象限内相交于点
在第象限内相交于点![]() ,半径为
,半径为![]() 的圆与
的圆与![]() 在第一象限内相交于点
在第一象限内相交于点![]() 按照此规律,则点
按照此规律,则点![]() 的坐标是( )
的坐标是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com