
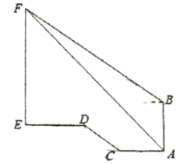
【题目】学校某数学兴趣小组想测学校旗杆高度如图,明明在稻香园一楼![]() 点测得旗杆顶点
点测得旗杆顶点![]() 仰角为
仰角为![]() ,在稻香园二楼
,在稻香园二楼![]() 点测得点
点测得点![]() 的仰角为
的仰角为![]() .明明从
.明明从![]() 点朝旗杆方向步行
点朝旗杆方向步行![]() 米到
米到![]() 点,沿坡度
点,沿坡度![]() 的台阶走到点
的台阶走到点![]() ,再向前走
,再向前走![]() 米到旗杆底部
米到旗杆底部![]() ,已知稻香园
,已知稻香园![]() 高度为
高度为![]() 米,则旗杆
米,则旗杆![]() 的高度约为( )(参考数据:
的高度约为( )(参考数据:![]() ,
,![]() ,
,![]() )
)
A.![]() 米B.
米B.![]() 米C.
米C.![]() 米D.
米D.![]() 米
米
科目:初中数学 来源: 题型:
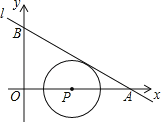
【题目】在直角坐标系中,我们将圆心坐标和半径均为整数的圆称为“整圆”.如图所示,直线l:y=kx+4![]() 与x轴、y轴分别交于A、B,∠OAB=30°,点P在x轴上,⊙P与l相切,当P在线段OA上运动时,使得⊙P成为“整圆”的点P个数是_____个.
与x轴、y轴分别交于A、B,∠OAB=30°,点P在x轴上,⊙P与l相切,当P在线段OA上运动时,使得⊙P成为“整圆”的点P个数是_____个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() ,交
,交![]() 轴于点
轴于点![]() .
.
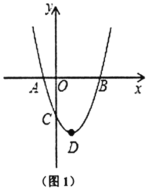
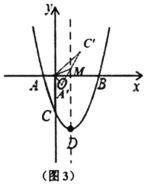
(1)抛物线顶点![]() 的坐标为________;
的坐标为________;
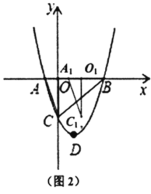
(2)如图2,连接![]() 、
、![]() .将
.将![]() 沿
沿![]() 轴方向以每秒1个单位长度的速度向右平移得到
轴方向以每秒1个单位长度的速度向右平移得到![]() ,运动时间为
,运动时间为![]() 秒.当
秒.当![]() 时,求
时,求![]() 与
与![]() 重叠面积
重叠面积![]() 与
与![]() 的函数解析式,并求出
的函数解析式,并求出![]() 的最大值;
的最大值;
(3)如图3中,将![]() 绕点
绕点![]() 顺时针旋转一定的角度
顺时针旋转一定的角度![]() 得到
得到![]() ,边
,边![]() 与抛物线的对称轴交于点
与抛物线的对称轴交于点![]() .在旋转过程中,是否存在一点
.在旋转过程中,是否存在一点![]() ,使得
,使得![]() ?若存在,直接写出所有满足条件的点
?若存在,直接写出所有满足条件的点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,平行四边形ABCD中,AB⊥AC,AB=3,AD=5,点P在边AD上运动,以P为圆心,PA为半径的⊙P与对角线AC交于A,E两点.
(1)如图2,当⊙P与边CD相切于点F时,求AP的长;
(2)不难发现,当⊙P与边CD相切时,⊙P与平行四边形ABCD的边有三个公共点,随着AP的变化,⊙P与平行四边形ABCD的边的公共点的个数也在变化,若公共点的个数为4,直接写出相对应的AP的值的取值范围.
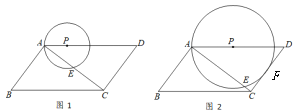
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BM是以AB为直径的⊙O的切线,B为切点,BC平分∠ABM,弦CD交AB于点E,DE=OE.

(1)求证:△ACB是等腰直角三角形;
(2)求证:OA2=OEDC:
(3)求tan∠ACD的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】只有1和它本身两个因数且大于1的正整数叫做素数.我国数学家陈景润哥德巴赫猜想的研究中取得了世界领先的成果.哥德巴赫猜想是“每个大于2的偶数都表示为两个素数的和”,如10=3+7.
(1)从7,11,13,17这4个素数中随机抽取一个,则抽到的数是11的概率是_____;
(2)从7,11,13,17这4个素数中随机抽取1个数,再从余下的3个数中随机抽取1个数,用画树状图或列表的方法,求抽到的两个素数之和等于24的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是一座立交桥的示意图(道路宽度忽略不计),A为入口,F,G为出口,其中直行道为AB,CG,EF,且AB=CG=EF;弯道为以点O为圆心的一段弧,且所对的圆心角均为90°.甲、乙两车由A口同时驶入立交桥,均以8m/s的速度行驶,从不同出口驶出,其间两车到点O的距离y(m)与时间x(s)的对应关系如图2所示,结合题目信息,下列说法错误的是( )
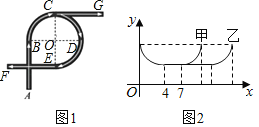
A.立交桥总长为168 m
B.从F口出比从G口出多行驶48m
C.甲车在立交桥上共行驶11 s
D.甲车从F口出,乙车从G口出
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com