如图.图中最大的扇形表示占的 %.可以量出这个扇形的圆心角 .如果不用量角器测量.请写出计算式: .如果知道该校学生人数总量为2000人.则可以算出最喜欢足球运动的有人．题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

如图，图中最大的扇形表示________占________的________％，可以量出这个扇形的圆心角________，如果不用量角器测量，请写出计算式：________，如果知道该校学生人数总量为2000人，则可以算出最喜欢足球运动的有________人．

答案：
解析：

喜欢足球的学生,全校学生,46,，×360＝,920

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

（2012•和平区模拟）图①至图③中，两平行线AB、CD间的距离均为6，点M为AB上一定点．扇形纸片OMP在AB、CD之间（包括AB、CD），扇形OMP的圆心角∠MOP=α，半径OM=4．如图①，扇形的半径OM在AB上．如图②③，将扇形纸片OMP绕点M在AB、CD之间顺时针旋转．
（Ⅰ）如图②，当α=60°时，在旋转过程中，点P到直线CD的最小距离是

，旋转角∠BMO的最大值是

90°

；
（Ⅱ）如图③，在扇形纸片OMP旋转的过程中，要使点P落在直线CD上，α的最大值是

120°

．

查看答案和解析>>

科目：初中数学 来源：2010年河北省初中毕业生升学文化课考试数学试题 题型：044

观察思考

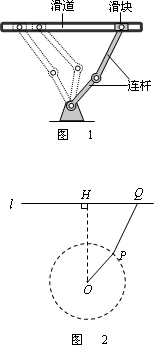
某种在同一平面进行传动的机械装置如图1，图2是它的示意图．其工作原理是：滑块Q在平直滑道l上可以左右滑动，在Q滑动的过程中，连杆PQ也随之运动，并且PQ带动连杆OP绕固定点O摆动．在摆动过程中，两连杆的接点P在以OP为半径的⊙O上运动．数学兴趣小组为进一步研究其中所蕴含的数学知识，过点O作OH⊥l于点H，并测得OH＝4分米，PQ＝3分米，OP＝2分米．

解决问题

(1)点Q与点O间的最小距离是________分米；点Q与点O间的最大距离是________分米；点Q在l上滑到最左端的位置与滑到最右端位置间的距离是________分米．

(2)如图3，小明同学说：“当点Q滑动到点H的位置时，PQ与⊙O是相切的．”你认为他的判断对吗？为什么？

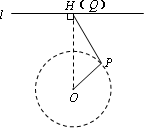
(3)①小丽同学发现：“当点P运动到OH上时，点P到l的距离最小．”事实上，还存在着点P到l距离最大的位置，此时，点P到l的距离是________分米；

②当OP绕点O左右摆动时，所扫过的区域为扇形，求这个扇形面积最大时圆心角的度数．

查看答案和解析>>

科目：初中数学 来源：2012届安徽省南陵县惠民中学九年级上学期第二次月考数学试卷（带解析） 题型：解答题

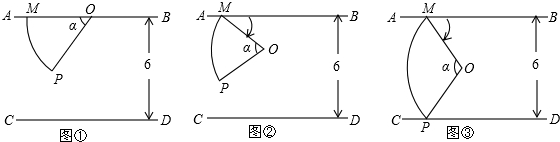
如图1至图4中，两平行线AB、CD间的距离均为6，点M为AB上一定点．

思考：
如图1，圆心为0的半圆形纸片在AB，CD之间（包括AB，CD），其直径MN在AB上，MN=8，点P为半圆上一点，设∠MOP=α。
当α=　　度时，点P到CD的距离最小，最小值为　　。
探究一：
在图1的基础上，以点M为旋转中心，在AB，CD 之间顺时针旋转该半圆形纸片，直到不能再转动为止，如图2，得到最大旋转角∠BMO=　　度，此时点N到CD的距离是　　。
探究二：
将如图1中的扇形纸片NOP按下面对α的要求剪掉，使扇形纸片MOP绕点M在AB，CD之间顺时针旋转。
（1）如图3，当α=60°时，求在旋转过程中，点P到CD的最小距离，并请指出旋转角∠BMO的最大值；
（2）如图4，在扇形纸片MOP旋转过程中，要保证点P能落在直线CD上，请确定α的最大值。